Вопрос 1
Информация и энтропия. Единицы их измерения
Мера количества информации характеризует степень уменьшения неопределенности (энтропии) об источнике сообщения.
Хартли предложил логарифмическую меру количества информации.
![]()
I – количество информации, М – число возможных сообщений
Достоинства меры Хартли:
- количество информации пропорционально длине сообщения (числу букв)
- количество информации от нескольких независимых источников равно сумме информаций от каждого источника
- удобна математически, т.к. при логарифмировании многие операции упрощаются
Недостаток меры Хартли:
- не учитывает вероятности возможных сообщений
Чем меньше вероятность события, о котором говориться в сообщении, тем оно больше несет информации.
Шеннон предложил количество информации,
которое несет одна буква ![]()
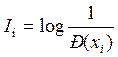
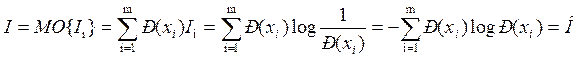
I – среднее количество информации
МО – математическое ожидание
Н – энтропия совокупности букв, у которых
вероятность ![]()
Если при получении сообщения неопределенность ликвидируется полностью, то I=H.
Если ликвидируется не полностью, то ![]()
Н – энтропия источника до получения сообщения
![]() - после
- после
Основание логарифма определяет единицу информации:
![]() - троичная единица
информации
- троичная единица
информации
![]() - десятичная (мера
Хартли)
- десятичная (мера
Хартли)
ln – натуральная (нат)
Вопрос 2
Основные свойства энтропии дискретных сообщений.
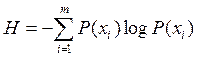 ,
, ![]()
![]() при
при 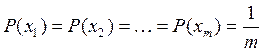
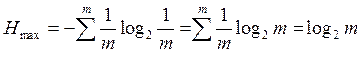
Таким образом,
максимальное значение энтропии равно логарифму возможных букв (![]() ).
).
Мера Хартли является правильной ( совпадает с мерой Шеннона) когда сообщения равновероятны.
X, Y – независимые источники (статистически)
![]()
Пусть источник:
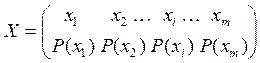 ,
, 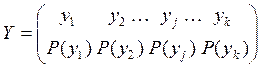
Найдем энтропию этих двух источников.
![]() - источник из 2 – х источников.
- источник из 2 – х источников.
![]()
![]()
Тогда имеем:
: 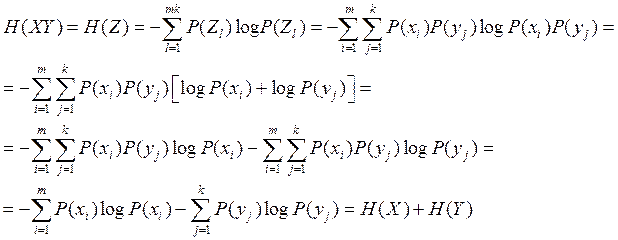
![]()
Пример статистически зависимых источников: рост и вес человека.
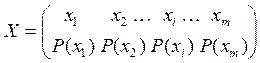 ,
,
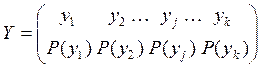
![]()
![]()
Далее находим энтропию двух источников ![]() и
и ![]()
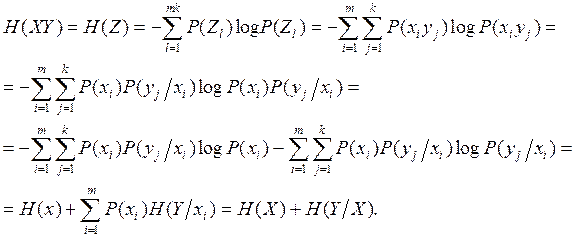
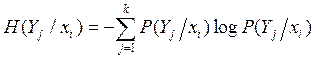 ; - частная
условная энтропия
; - частная
условная энтропия
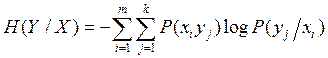 ; - условная
энтропия
; - условная
энтропия
![]()
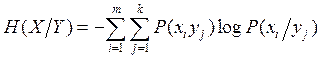
![]() ;
; ![]()
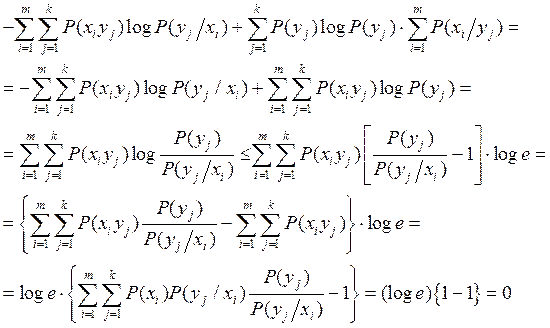
Значит источники статистически независимы.
6.
![]()
![]() , т.к.
, т.к. ![]()
Вопрос 3
Оптимальное кодирование источника. Код Шеннона-Фано. Кодовое дерево.
Кодирование при котором скорость передачи информации приближается к пропускной способности называется оптимальным, статистическим или эффективным.

Для оптимального кода нужно:
1. Чтобы буквы большей вероятности кодировались кодовыми комбинациями. В этом случае средняя длина кодовой комбинации будет минимальной.
2. Оптимальный код не требует разделительных знаков.
3. Вероятности 0 и 1 на выходе кодера должны быть примерно равны.
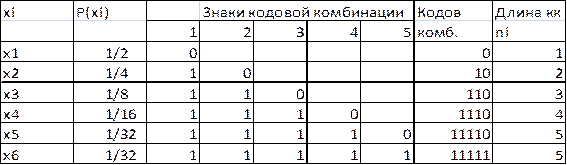
1. Располагаем буквы в порядке убывания их вероятности.
2. Все буквы делим на 2 группы с соблюдением примерного равенства суммарной вероятности этих групп
3. Буквам верхней группы присваиваем знак 0, а нижней 1.
4. Каждую группу разбиваем на 2 подгруппы с соблюдением примерно такого же равенства суммарной вероятности.
5. Буквам верхней подгруппы-0, нижней-1
6. Повторим 4 и 5, пока в каждой подгруппе не останется по 1 букве.
Вычислим среднюю длину кК:
nср= МО{ni}=![]() (xi)ni=
(xi)ni= ![]()
Вычислим энтропию источника сообщения:
![]()
R=C, т.к. один бит информации кодируется одном знаком.
Чтобы код не требовал разделенных знаков, никакая его кодовая комбинация не должна быть началом другой.
Строение кода удобно изобразить в виде кодового дерева
Правило построения кодового дерева: из каждого узла, как правило, исходное число ветвей, равное основанию кода. Шаг вправо – 0, влево – 1. Длина ветвей не имеет значения. Используемые кК обозначают кружочками. Дерево строят начиная с вершины.
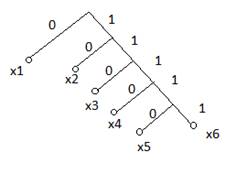
Код не требует раздельных знаков, если на концах ветвей кодовые комбинации.
0,1,2
Вопрос 4
Пропускная способность дискретного канала с помехами
Канал называют дискретным, если его входные и выходные сигналы дискретны. Свойства канала определены, если заданы.
1) Алфавиты входных и выходных сигналов.
Входные сигналы: S1, S2, …Si, …, Sm;
Выходные сигналы: S1*, S2*, …, Si*,…Sm*
В общем случае m=m*
Существует стирающий канал, в котором m*= m+1. Это сигнал неопределённости.
Пример:
|
2)Техническая скорость передачи сигнала.
![]() Где
Где ![]() .
.
3)P (Sj*/ Si)- вероятность перехода.
Вероятность перехода удобно располагать в виде канальной матрицы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.