Глава5Уравнение плоскости. Уравнение прямой в пространстве.
5.1 Виды уравнения плоскости.
5.1.1 Общее уравнение плоскости.
Ах+Ву+Сz+D=0
Коэффициенты А, В, С в этом уравнении определяют так
называемый нормальный вектор ![]() , перпендикулярный
плоскости, то есть являются его проекциями на оси декартовой системы координат
, перпендикулярный
плоскости, то есть являются его проекциями на оси декартовой системы координат ![]() . Приравнивая к нулю различные
коэффициенты мы получаем частные виды общего уравнения плоскости.
. Приравнивая к нулю различные
коэффициенты мы получаем частные виды общего уравнения плоскости.
а)![]() - уравнение
плоскости принимает вид: Ах+Ву+Сz=0, такая плоскость проходит через начало
координат.
- уравнение
плоскости принимает вид: Ах+Ву+Сz=0, такая плоскость проходит через начало
координат.
б)![]() - получаем
уравнение: Ву+Сz+D=0, плоскость параллельна оси ОХ. Если коэффициент D=0:
- получаем
уравнение: Ву+Сz+D=0, плоскость параллельна оси ОХ. Если коэффициент D=0:
Ву+Сz=0 – то плоскость проходит через ось ОХ.
в) ![]() - получаем
уравнение Ах+СZ+D=0 плоскость параллельна оси ОУ. В случае, если и коэффициент D=0:
- получаем
уравнение Ах+СZ+D=0 плоскость параллельна оси ОУ. В случае, если и коэффициент D=0:
Ах+СZ=0 – плоскость координат проходит через ось ОУ.
г) ![]() - получаем
уравнение Ах+Ву+D=0 плоскость параллельна оси ОZ. В случае равенства нулю коэффициента D=0:
- получаем
уравнение Ах+Ву+D=0 плоскость параллельна оси ОZ. В случае равенства нулю коэффициента D=0:
Ах+Ву=0 – плоскость проходит через ось ОZ.
д) ![]()
CZ+D=0 – плоскость параллельна координатной плоскости ХОУ
е) ![]()
AX+D=0 – плоскость параллельна координатной плоскости УОZ.
ж) ![]()
ВУ+D=0 – плоскость параллельна координатной плоскости ХОZ.
5.1.2 Уравнение плоскости проходящей через заданную точку перпендикулярную заданному вектору.
Пусть задана точка ![]() и
вектор
и
вектор ![]() (Рис. 5.1)
(Рис. 5.1)
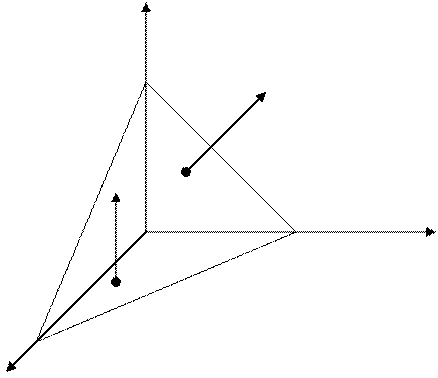 z
z
![]()
p
y
x
Возьмем произвольную точку М (х,у,z),
принадлежащую искомой плоскости Р. найдём проекции вектор ![]() лежащего в плоскости Р.
лежащего в плоскости Р.
![]()
По условию вектор ![]() перпендикулярен
плоскости Р, следовательно вектор
перпендикулярен
плоскости Р, следовательно вектор ![]() перпендикулярен
вектору
перпендикулярен
вектору ![]() . Используя условие
перпендикулярности двух векторов получим
. Используя условие
перпендикулярности двух векторов получим ![]() .
Представляя скалярное произведение в координатной форме получим искомое
уравнение.
.
Представляя скалярное произведение в координатной форме получим искомое
уравнение.
А(х-х0)+В(у-у0)+С(z-z0)=0
5.1.3 Уравнение плоскости проходящей через три заданные точки.
Пусть заданы три точки принадлежащие искомой плоскости Р М1(х1,у1,z1); М2(х2,у2,z2); М(х3,у3,z3). (Рис. 5.2)
![]() z
z
 |
p
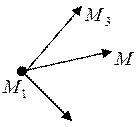 |
![]()


![]() y
y
|
|
Возьмём произвольную точку М(x,y,z) принадлежащую искомой прямой Р.
Рассмотрим векторы: ![]()
![]()
![]()
![]()
Так как точки М1, М2, М3,
М лежат в одной плоскости, то векторы ![]() -
коллинеарные, следовательно их смешанное произведение равно нулю.
-
коллинеарные, следовательно их смешанное произведение равно нулю.
![]()
Представляя это произведение в координатной форме, получим искомое уравнение:
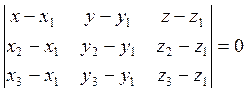
1. Уравнение плоскости в отрезках.
Рассмотрим плоскость пересекающую все три координатные оси и не проходящую через начало координат. Запишем уравнение этой плоскости в общем виде.
Ах+Ву+Сz+D=0
![]()
Пусть а, b, с длины отрезков отсекаемые плоскостью на осях координат (Рис. 5.3)
z
 R
R
Q

![]() 0 y
0 y
P х
Рис 5.3
Точка Р(0,0,0) лежит на плоскости поэтому она обращает уравнение плоскости в тождество.
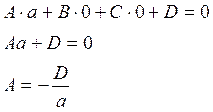
аналогично точка Q(0,b,0) лежит на плоскости, из этого следует
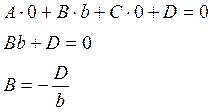
аналогично точка R(0,0,c) лежит на плоскости.
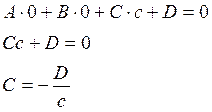
Подставляя найденные значения коэффициентов в уравнение плоскости получим:
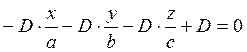
так как по условию D не равно нулю, то полученное уравнение можно сократить на D.
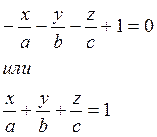
Полученное уравнение называется уравнением плоскости в отрезках.
5.2 Угол между двумя плоскостями. Условие параллельности и перпендикулярности двух плоскостей. Расстояние от точки до плоскости.
Пусть уравнения двух плоскостей заданы в виде:
А1х+В1у+С1z+D1=0
А2х+В2у+С2z+D2=0
Угол между этими плоскостями равен углу между нормальными векторами
этих плоскостей ![]() и может быть найден из
известного выражения :
и может быть найден из
известного выражения :
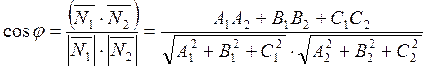
Если две плоскости перпендикулярны, то угол между
векторами ![]() равен 900 отсюда
следует условие перпендикулярности плоскостей.
равен 900 отсюда
следует условие перпендикулярности плоскостей.
![]()
Если две плоскости параллельны, то нормальные векторы ![]() параллельны и условие
параллельности двух плоскостей сводится к условию колинеарности векторов
параллельны и условие
параллельности двух плоскостей сводится к условию колинеарности векторов ![]() .
.
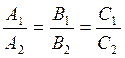
Пусть задана точка М1(х1,у1,z1) и плоскость Ах+Ву+Сz+D=0. Формула расстояния от точки М1 до заданной плоскости определяется формулой:
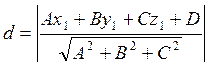
5.3 Виды уравнений прямой в пространстве.
5.3.1 Каноническое уравнение прямой в пространстве.
Пусть задана точка М0(x0,y0,z0) и вектор ![]() ,
параллельный искомой прямой и называемой направляющим вектором прямой. (Рис.
5.4)
,
параллельный искомой прямой и называемой направляющим вектором прямой. (Рис.
5.4)
z![]()
 |

0
![]() y
y
x
На прямой возьмём произвольную точку М (x,y,z) и рассмотрим вектор ![]() . Вектор
. Вектор ![]() параллелен
параллелен ![]() . Из условия параллельности двух
векторов следует:
. Из условия параллельности двух
векторов следует:
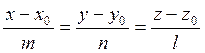
Полученные уравнения называются каноническими уравнениями прямой в пространстве.
5.3.2 Параметрические уравнения прямой.
Приравнивая в канонических уравнениях прямой каждую из дробей некоторому параметру t:
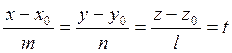
Получим уравнения выражающие текущие координаты каждой точки прямой через параметр t.
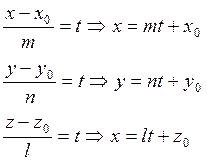
таким образом параметрические уравнения прямой имеют вид:
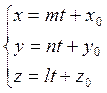
5.3.3 Уравнения прямой проходящей через две заданные точки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.