Симметричная положительно определенная матрица. Условие несмещенности прогноза

Прогнозирование

Пусть  – известные значения,  – неизвестно.

Будем считать, что основные гипотезы имеют место также для «наблюдения» :

1)                          (52)

2)                                  (53)

3) ,                         (54)

где ,   – симметричная положительно определенная матрица размера , такая, что  – ее подматрица,

4)                         (55)

При заданном  будем строить прогноз, линейный относительно :

                                         (56)

где .

Условие несмещенности прогноза имеет вид:

                         (57)

Из (1), (2), (56):

            

Итак,

                                         (58)

Из (52), (53):

                              (59)

Итак, условие несмещенности прогноза (56) имеет вид:

                                              (60)

Поскольку равенство (60) должно выполняться при всех , из него следует, что:

                           (61)

Условие эффективности прогноза заключается в том, что вектор  обеспечивает минимум выражения:

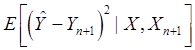                                (62)

В силу (60):

          (63)

Следовательно,

                            (64)

Подставим (64) в (62) и воспользуемся формулой (3):

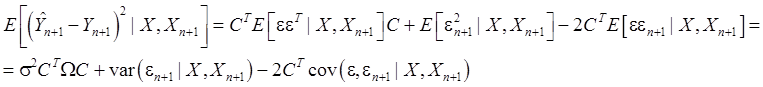
Итак,

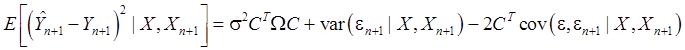     (65)

Заметим, что  равен произведению  на элемент  матрицы , а  вектор-столбец  равен произведению  на столбец  соответствующих элементов матрицы .

Следовательно, равенство (65) можно также записать в виде:

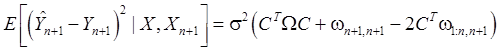                  (66)

Таким образом, вектор  обеспечивающий несмещенный и эффективный прогноз в классе прогнозов, линейных относительно , является решением следующей оптимизационной задачи:

                          (67)

                                       (68)

Построим функцию Лагранжа для задачи (67)-(68):

                (69)

где  – вектор множителей Лагранжа.

Продифференцируем функцию Лагранжа по .

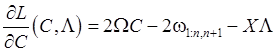                           (70)

Приравняв полученное выражение к нулю, получим условие Куна-Таккера:

                                         (71)

Таким образом, задача свелась к решению системы уравнений (68), (71) относительно векторов  и  :

,                                              (72)

                                                              (73)

Умножим уравнение (72) слева на  и выразим из полученного равенства вектор :

                            (74)

Подставим эту формулу в (73):

                    (75)

Отсюда:

                 (76)

Подставим (76) в (74):

              (77)

Формула (77) дает оптимальное решение оптимизационной задачи (67), (68).

Следовательно, эффективный несмещенный прогноз вычисляется с помощью вектора (77) по формуле (56):

                                                     (78)

Из формул (5), (18), (19), (77) следует, что формула (78) может быть также представлена в виде:

                                                    (79)

Отметим, что в случае классической модели (когда )  и . Следовательно, для случая классической модели формула (79) принимает вид: , что согласуется с полученными ранее результатами.

В случае, когда присутствует только гетероскедастичность (а автокорреляция отсутствует), матрица  диагональна и . Следовательно, в этом случае формула (79) имеет вид:

                                       (80)

Интервальная оценка для

Заметим, что в силу (52), (53):

                                          (81)

В силу несмещенности ОМНК-оценки :

                                      (82)

Из результатов для классической модели следует, что случайные величины  и  независимы. Следовательно, случайные величины  и  также независимы. Поэтому в силу (22’), (82) случайная величина:

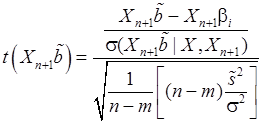                                          (83)

имеет распределение Стъюдента со степенями свободы  .

Упростив (83), получим:

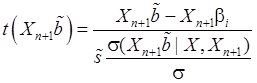                                           (84)

Найдем стандартное отклонение   случайной величины .

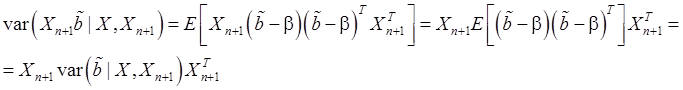
Итак,

                             (85)

Подставим (17) в (85):

                              (86)

Из (86):

                                (87)

В силу (86), (87) в качестве оценок дисперсии и стандартного отклонения случайной величины  возьмем: