Получение навыков количественных оценок эффектов и явлений в структуре полупроводников и интегральных микросхем, страница 9

Вывод: наложение дополнительных ограничений в виде периодичности потенциальных силовых полей кристаллической решетки приводит к решению уравнения Шредингера в виде, из которого вытекает зонная структура энергетического спектра микрочастицы в периодическом силовом поле. При этом в пределах каждой зоны спектр энергии является непрерывным.

К – это характеристика барьера, характеризующая степень связанности электрона с ионом кристаллической решетки. Уменьшение К может быть следствием уменьшения высоты барьера при неизменной ширине.

Выразив энергию из уравнения (2), получим:

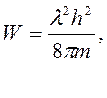
то есть энергия электрона может меняться непрерывно, так как l = а в пределах от нуля до .

При энергия частицы совпадает с энергией свободной частицы, так как находится в среде без потенциального барьера (условие отсутствия связи).

Пусть  , что может быть обусловлено только тем, что при неизменной ширине барьера значение  высоты барьера будет бесконечно большим (условие сильной связи). Тогда  = np, где n = 0,1, 2, 3…Найдем для соответствующие значения

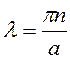, тогда энергия частицы может быть представлена как

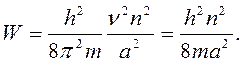
То есть мы получили то же выражение, как и для потенциального ящика, находящегося не в периодической структуре, то есть для сильно связанного электрона. Энергия такой частицы может принимать только дискретные значения.

Рассмотрим случай сильной, но не бесконечно большой связи, когда не исключается возможность перемещения электрона кристаллической структуре. Аргумент, при котором наблюдается несоответствие: где  - малая величина. Тогда так как  и то

.

         вблизи np принимает значения, близкие к единице, следовательно,  = (-1)ⁿ. В результате исходное выражение можно записать в виде:

.

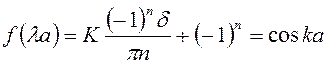В результате упрощений случай сильной связи мы свели к виду, где нет тригонометрических функций.

Разрешённые значения энергий в n-ой зоне:

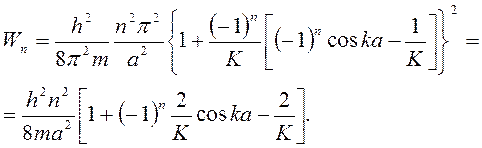
Это означает, что для каждой зоны разрешённых значений модель энергетических уровней принимает вид:

Это соотношение является фундаментальным уравнением (моделью)  для n-ой энергетической зоны. Значение его состоит в том, что его применение позволяет объяснить наиболее важные фундаментальные свойства твёрдого тела с учётом особенностей кристаллической структуры на количественном уровне.

Лекция № 10

Энергетический спектр электронов в периодической структуре

,

где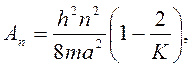

К – характеристика барьера, а – ширина потенциальной ямы, b – ширина барьера;

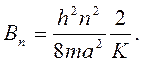
A_n – некоторая энергия, соответствующая середине зоны, B_n – амплитуда, отклонение от среднего значения.

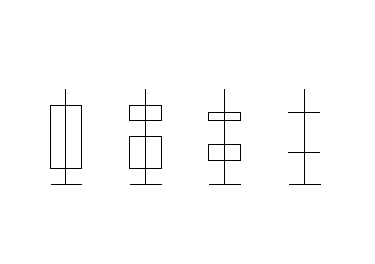при изменении волнового числа от нуля до рассматриваются все значения энергии в предыдущей зоне.

Для случая, когда , A_n и B_n стремятся к бесконечным значениям, значит, ширина зоны увеличивается.

По мере увеличения К, B_n уменьшается, то есть среднее значение энергии смещается вверх: энергетический    спектр трансформируется в отдельные зоны, со своим средним уровнем. По мере дальнейшего увеличения К, зоны стягиваются в отдельные дискретные уровни, что характерно для электронов, находящихся в различных слоях атомной структуры, сильно связанных с ядром атома.

Полученная модель охватывает все практически значимые случаи: от слабых до сильных связей, и отражает общую закономерность: по мере увеличения степени связности зоны сужаются, переходя в пределе в отдельные дискретные уровни. Этот результат получен с учетом того, что имеются потенциальные барьеры, которые периодически повторяются в структуре, а также с учетом вероятности нахождения частицы как над барьером, так и в пределах ящика. Рассмотрим уточнения, которые вносятся в модель с учётом периодичности внутренней структуры. Рассматривая математическую сторону, наложение условия Борна-Кармано () можно интерпретировать так (рассмотрим координатную часть):

.

Пусть

тогда

, значит , а это возможно тогда и только тогда, когда