и тогда получим такое уравнение для dp/dt:
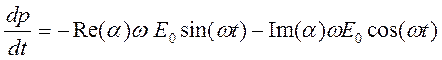
Усредненное по времени значение рассеянной энергии можно затем получить путем перемножения этих двух выражений и образования среднего на некотором временном интервале. В результате получим следующее выражение:
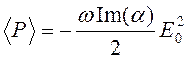
Теперь введем понятие сечения поглощения, которое обозначим символом___________. Оно определяется таким образом, что если электромагнитное излучение с плотностью потока F падает на частичку, то средняя поглощенная энергия равна
Применяя уравнения (2.4), (2.7) и (2.8), найдем выражение для сечения поглощения:
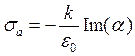
где к — волновое число излучения. Понятно, что __________ имеет размерность площади, и эта площадь обладает физической интерпретацией, смысл которой в том, что частица как бы поглощает все излучение, падающее на площадь сечения. Из уравнения (3.75) также следует, что мнимая составляющая поляризуемости не может быть отрицательной.
Для малой сферической частицы радиуса а при коэффициенте преломления п (который может быть комплексным) поляризуемость выражается формулой
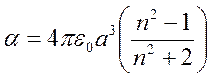
и, следовательно, отношение сечения поглощения к геометрическому сечению ________________ составляет
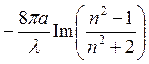
С учетом нашего условия, что радиус _________ частицы существенно меньше длины волны ________, значение этого выражения должно быть гораздо меньше 1. Таким образом, частички малого размера поглощают намного меньше энергии, чем содержится в излучении, которое проходит через сечение, по площади соответствующее геометрическим размерам частицы.
Рассмотрим теперь рассеяние на наших малых _____________ частичках. Согласно законам классической электродинамики осциллирующий электрический диполь, мощность которого описывается уравнением
излучает среднюю энергию
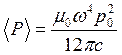
Следовательно, для частицы, обладающей поляризуемостью ____________ и находящейся в электромагнитном поле
средняя переизлученная мощность составляет
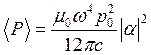
Мы можем ввести понятие сечение рассеяния _____________, подобно тому, как сделали для сечения поглощения, т. е. приняв энергию рассеяния равной _______________, если на частицу падает излучение с плотностью потока F. Обращаясь снова к уравнениям (2.4), (2.7) и (2.8), получим:
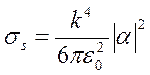(3.77)
Как и в случае с сечением поглощения, сечение рассеяния гораздо меньше по площади геометрического сечения частицы, конечно, при условии малости размеров частицы по сравнению с длиной волны излучения.
Мы уже отмечали в п. 3.4.1, что для описания рассеянного излучения необходимо знать, какая распределена энергия, отражаемая в различных направлениях. С этой целью в уравнение (3.65) была введена фазовая функция. Для рассеяния малыми частицами, описываемого выражением (3.77), фазовая функция имеет вид:
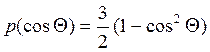(3.78)
(Учтите, здесь р вовсе не обозначает электрический дипольный момент!)
Уравнение (3.78) показывает, что рассеяние максимально в направлениях по и против хода излучения (________________________________) и равно нулю в направлении ________. Коэффициент 3/2 введен с целью нормализации, чтобы интеграл по всем направлениям был равен 4л. Для сравнения заметим, что фазовая функция при изотропном рассеянии равна 1 во всех направлениях.
Уравнения (3.75), (3.77) и (3.78) применимы только тогда, когда размеры частиц существенно меньше длины волны излучения. В этом случае явление носит название рассеяния Рэлея. При частицах большего размера ситуация усложняется. Если частицы имеют сферическую форму радиусом ______________, задачу иногда можно решить, вводя безразмерную переменную
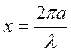
Тогда рассеяние Рэлея будет соответствовать случаю малости х. При больших значений х применяется теория рассеяния Ми. В этом случае ослабление (аттенуация) и сечение рассеяния можно представить выражениями:
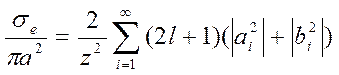(3.79)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.