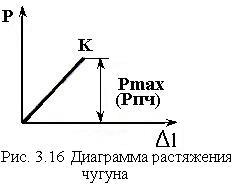
 Диаграмма
растяжения чугуна носит прямолинейный характер, при этом разрыв образца
происходит без пластических деформаций (рис. 3.16). По диаграмме растяжения
можно определить максимальную нагрузку
Диаграмма
растяжения чугуна носит прямолинейный характер, при этом разрыв образца
происходит без пластических деформаций (рис. 3.16). По диаграмме растяжения
можно определить максимальную нагрузку ![]() ,
по которой определяют единственную характеристику прочности – предел прочности
,
по которой определяют единственную характеристику прочности – предел прочности 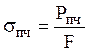 .
.
в) испытание на сжатие малоуглеродистой стали
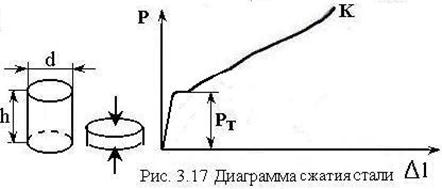 Диаграмма сжатия
образцов из малоуглеродистой стали (рис. 3.17) похожа на диаграмму растяжения
той же стали но при этом точка
Диаграмма сжатия
образцов из малоуглеродистой стали (рис. 3.17) похожа на диаграмму растяжения
той же стали но при этом точка ![]() соответствует
не разрыву образца, а прекращению испытаний. При этом образец может быть доведен
до сильно сплюснутого состояния, не разрушаясь. Пределы текучести на растяжение
и сжатие образцов из одного и того же высокопластичного материала примерно
одинаковы:
соответствует
не разрыву образца, а прекращению испытаний. При этом образец может быть доведен
до сильно сплюснутого состояния, не разрушаясь. Пределы текучести на растяжение
и сжатие образцов из одного и того же высокопластичного материала примерно
одинаковы: ![]()
г) испытание на сжатие чугуна
 Диаграмма сжатия
чугуна (рис 3.18) имеет близкий к прямолинейной зависимости характер, при этом
разрушение образца происходит с малыми пластическими деформациями с
образованием трещины под углом в 45 градусов к линии нагружения (в этой
площадке действуют наибольшие касательные напряжения). Предел прочности при
сжатии, определяемый по наибольшей нагрузке, значительно больше предела
прочности при растяжении:
Диаграмма сжатия
чугуна (рис 3.18) имеет близкий к прямолинейной зависимости характер, при этом
разрушение образца происходит с малыми пластическими деформациями с
образованием трещины под углом в 45 градусов к линии нагружения (в этой
площадке действуют наибольшие касательные напряжения). Предел прочности при
сжатии, определяемый по наибольшей нагрузке, значительно больше предела
прочности при растяжении: ![]() .
.
3.7 Пример выполнения расчетно-графической работы № 2.1: Осевая деформация стержня переменного сечения
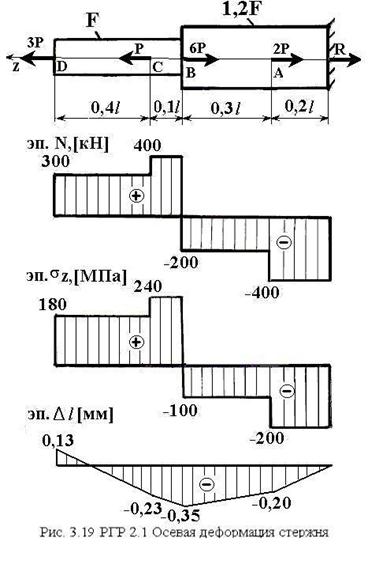 Дано:
Дано: 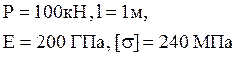
Задание (рис. 3.19):
1) построить эпюру осевых сил N(z)
2) построить эпюру
нормальных напряжений ![]()
1)
определить минимально необходимую площадь поперечного
сечения ![]() из
условия прочности по нормальным напряжениям
из
условия прочности по нормальным напряжениям
4) построить эпюру
абсолютных удлинений ![]()
Решение.
1) Заменяя
жесткую заделку на реакцию ![]() ,
и совмещая начало координат с неподвижным концом стержня, составляем уравнение
равновесия всех сил на ось стержня:
,
и совмещая начало координат с неподвижным концом стержня, составляем уравнение
равновесия всех сил на ось стержня:
![]() (реакция
в заделке направлена в противоположную сторону по отношению к показанному на
рисунке)
(реакция
в заделке направлена в противоположную сторону по отношению к показанному на
рисунке)
Выражение для осевых сил (для 4-х участков стержня):
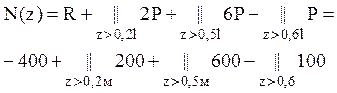 .
.
Символ ![]() означает,
что слагаемое, следующее за ним, следует учитывать только при превышении осевой
координаты указанного значения.
означает,
что слагаемое, следующее за ним, следует учитывать только при превышении осевой
координаты указанного значения.
Строим эпюру осевых сил, которая является кусочно-постоянной функцией и меняется скачкообразно в точках приложения сосредоточенных сил.
2) Выражение для осевых сил и нормальных напряжений для каждого из участков в отдельности:
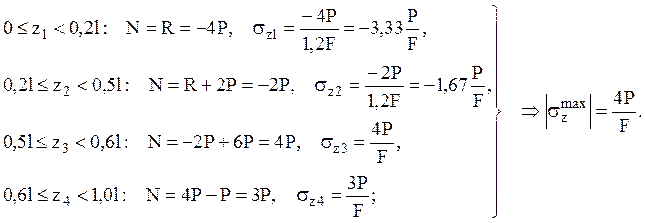
3) Условие прочности при одноосном
растяжении-сжатии:
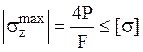
Определяем минимально-необходимую площадь поперечного сечения
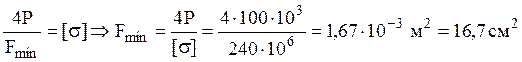
3) Определяем значения нормальных напряжений для найденного значения площади сечения:
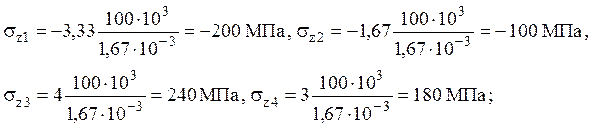
Строим эпюру нормальных напряжений, которая является постоянной для участков, где отношение осевой силы к площади сечения одинаково.
4) Определяем абсолютные удлинения участков стержня
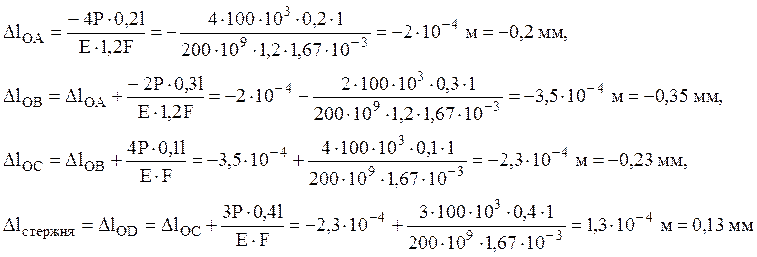
(следовательно, в целом, стержень удлиняется)
Строим эпюру продольных перемещений, которая является кусочно-линейной функцией.
4. Кручение стержней круглого поперечного сечения
4.1 Деформация кручения
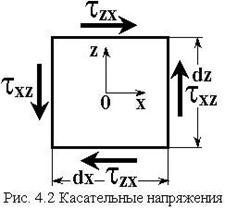
 Деформация сдвига
определяется изменением первоначально прямого угла между элементами. Данное
изменение равно углу
сдвига
Деформация сдвига
определяется изменением первоначально прямого угла между элементами. Данное
изменение равно углу
сдвига ![]() (рис. 4.1).
(рис. 4.1).
Чистый сдвиг – напряженно-деформированное состояние, характеризуемое тем, что на гранях элемента возникают только касательные напряжения.
Пусть ![]() -
абсолютный сдвиг, тогда
-
абсолютный сдвиг, тогда ![]() - относительный
сдвиг (угол сдвига)
- относительный
сдвиг (угол сдвига)
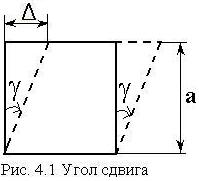
Закон парности касательных напряжений – на взаимно-перпендикулярных площадках касательные напряжения численно равны и направлены так, что стремятся вращать элемент в противоположные стороны.
Составим уравнение равновесия по моментам относительно центра бесконечно-малого элемента единичной толщины выделенного из деформированного тела (рис. 4.2):
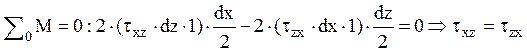 ,
,
аналогично ![]() .
.
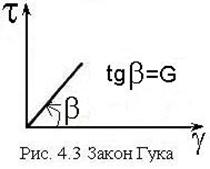
Закон Гука при сдвиге:
при малых деформациях касательные напряжения пропорциональны вызываемому ими
углу сдвига: ![]() , где
, где ![]() -
модуль упругости материала при сдвиге (модуль сдвига)
-
модуль упругости материала при сдвиге (модуль сдвига)
 Для изотропного
материала три упругих константы связаны соотношением:
Для изотропного
материала три упругих константы связаны соотношением: 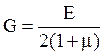 .
.
Для Ст3: (![]() ):
):
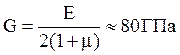 .
.
4.2 Формула для касательных напряжений
Допущения:
- гипотеза плоских
сечений: все поперечные сечения, поворачиваясь вокруг оси ![]() , остаются плоскими.
, остаются плоскими.
 - гипотеза прямых
радиусов: все радиусы данного сечения остаются прямыми и
поворачиваются на один и тот же угол
- гипотеза прямых
радиусов: все радиусы данного сечения остаются прямыми и
поворачиваются на один и тот же угол ![]() - угол
закручивания (см. рис. 4.4а).
- угол
закручивания (см. рис. 4.4а).
На рис. 44а видно, что ![]() . Отсюда относительный
(погонный) угол закручивания определяется по формуле
. Отсюда относительный
(погонный) угол закручивания определяется по формуле 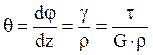 , а угол сдвига
, а угол сдвига 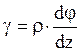
Суммарный момент от касательных
напряжений равен заданному моменту: 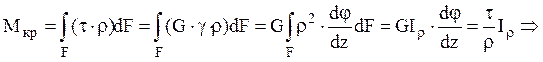
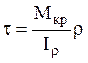 и
и
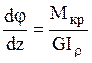 где
где ![]() -
жесткость круглого поперечного сечения при кручении.
-
жесткость круглого поперечного сечения при кручении.
где ![]() - расстояние от центра
сечения до произвольной точки.
- расстояние от центра
сечения до произвольной точки.
Условие прочности при кручении: 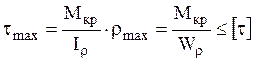 , где
, где 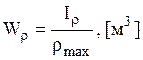 -
момент сопротивления при кручении.
-
момент сопротивления при кручении.
 для сплошного
круглого сечения:
для сплошного
круглого сечения: 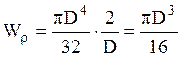 ,
,
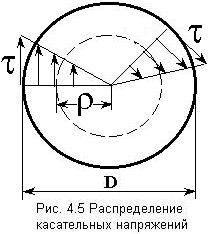 для полого
толстостенного сечения:
для полого
толстостенного сечения: 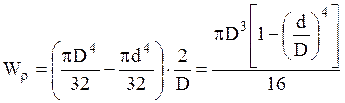 ,
,
для тонкостенного кольцевого сечения: 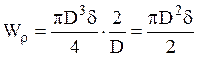 .
.
Правило знаков при кручении: крутящий момент положителен, если при наблюдении со стороны внешней нормали к поперечному сечению, он поворачивает сечение по часовой стрелке (рис. 4.4б).
Касательные напряжений при кручении изменяются вдоль радиуса по линейному закону (рис. 4.5): в центре сечения они равны нулю, а наибольших значений достигают на контуре сечения.
Угол закручивания определяется по
формуле 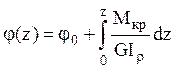 , где
, где ![]() - угол поворота в начале
координат. При
- угол поворота в начале
координат. При ![]() и
и ![]() :
: 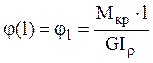 .
.
Пример.
1) Определить крутящий момент,
передаваемый валопроводом корабля на винт, если ![]() -
мощность двигателя
-
мощность двигателя ![]() и
и ![]() -
частота вращения валопровода
-
частота вращения валопровода  известны.
известны.
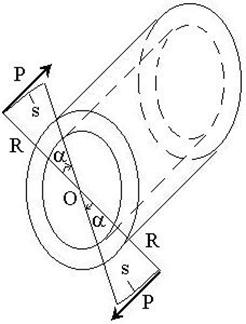 2) Определить
внутренний
2) Определить
внутренний ![]() и наружный диаметры
и наружный диаметры ![]() валопровода из условия прочности по
касательным напряжениям при
валопровода из условия прочности по
касательным напряжениям при 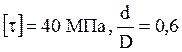 .
.
Решение:
1) Работа пары сил ![]() , создающей крутящий момент
, создающей крутящий момент ![]() равна
равна ![]() .
.
![]() оборотам
в минуту соответствует угол, равный
оборотам
в минуту соответствует угол, равный ![]() рад. Работа
в единицу времени определяет мощность двигателя:
рад. Работа
в единицу времени определяет мощность двигателя: 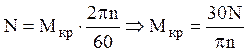 .
.
Для 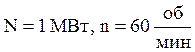 :
:
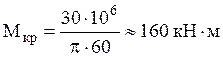 .
.
2) Из условия прочности определяем
наружный диаметр 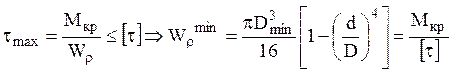 и
и 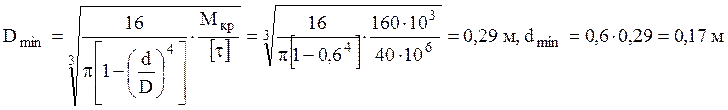 .
.
4.3 Пример выполнения расчетно-графической работы № 2.2: Внутренние усилия и перемещения при кручении
Дано: сплошной вал с ![]() (рис. 4.6)
(рис. 4.6)
Необходимо:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.