Конспект лекционных и практических занятий по дисциплине "Сопротивление материалов", страница 10

5.5 Условие прочности по касательным напряжениям

а) прямоугольник

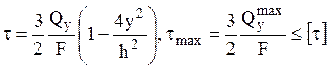
б) круг

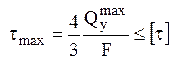
в) двутавр и швеллер

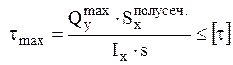, где  - толщина стенки сечения.

При этом распределение касательных напряжений по ширине полок у данных сечений линейно, поскольку координата центра тяжести для любой отсеченной площади одинакова, а сама площадь увеличивается линейно (рис. 5.6).

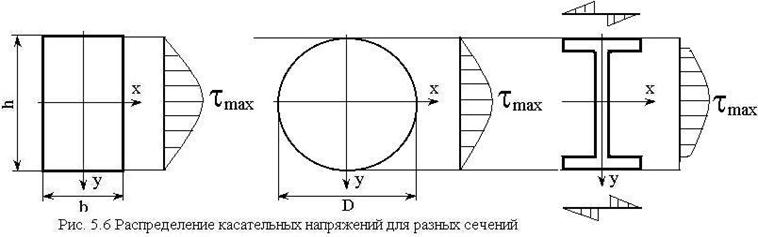
При решении задач вначале проверяют выполнение условия прочности по нормальным напряжениям (или выбирают минимально-необходимое сечение исходя из условия выполнения данного условия прочности), а затем осуществляют проверку выполнения условия прочности по касательным напряжениям.

5.6 Пример выполнения расчетно-графической работы № 3: Построение эпюр внутренних усилий и расчет прочности при изгибе статически-определимых балок

I) (шарнирно-опертая балка)

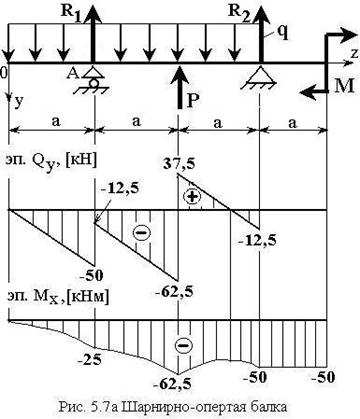
Для шарнирно-опертой балки (рис.5.7а) при ,

1) найти реактивные усилия

2) записать выражения и построить эпюры поперечных сил и изгибающих моментов

3) выбрать поперечное сечение в форме двух швеллеров из условия прочности по нормальным напряжениям с проверкой выполнения условия прочности по касательным напряжениям

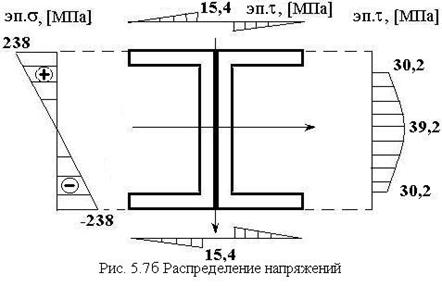
4) построить распределения нормальных и касательных напряжений для выбранного профиля

Решение:

Совмещаем начало координат с левым концом балки

1. Определение реакций опор:

Сумма всех сил на вертикальную ось:

Сумма моментов относительно точки A:

; .

2. Выражения для поперечной силы и изгибающего момента

а) по участкам

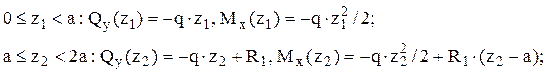
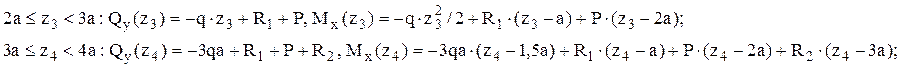б) Выражения для поперечной силы и изгибающего момента в одну строку:

;

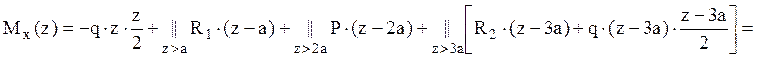
Заносим значения внутренних усилий в характерных точках в таблицу и строим эпюры

Определяем координату на третьем участке , где поперечная сила равна нулю: -, при этом  имеет максимум.

3. Выбор поперечного сечения

Опасное сечение по нормальным напряжениям : ,

опасное сечение по касательным напряжениям : .

Из условия прочности по нормальным напряжениям определяем минимально необходимый момент сопротивления поперечного сечения:

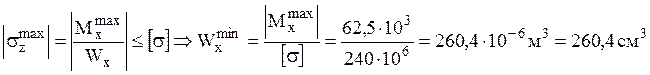для одного швеллера. По сортаменту находим швеллер № 18a, у которого момент сопротивления.

Проверяем выполнение условия прочности по касательным напряжениям

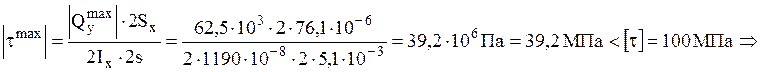
условие прочности по касательным напряжениям выполнено.

Определяем значения касательных напряжений для точек 2, 3:

Точка 1:

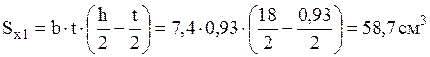
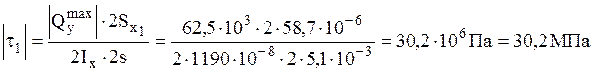
Точка 2:

.

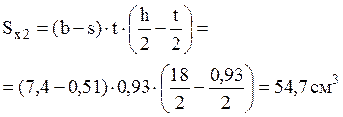
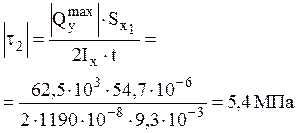По полученным точкам строим распределения напряжений (рис. 5.7б)

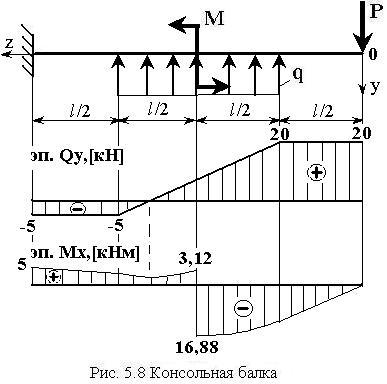
II) консольная балка

Для консольной балки (см. рис.5.8) для ,

1) записать выражения и построить эпюры поперечных сил и изгибающих моментов

2) проверить выполнение условий прочности по нормальным и касательным напряжениям для сечения в виде двух швеллеров № 10

Решение:

Совмещаем начало координат с правым свободным концом балки (в этом случае не нужно определять реакции, возникающие в заделке)

1. Выражения для поперечной силы и изгибающего момента

а) по участкам

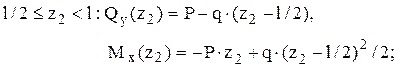
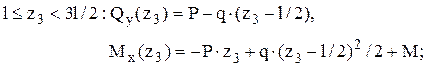
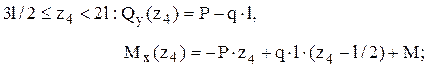
б) в одну строку

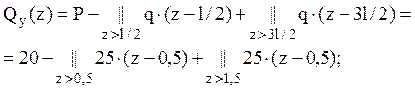
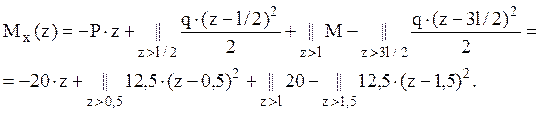
Заносим значения внутренних усилий в характерных точках и строим эпюры

Определяем координату на третьем участке , где поперечная сила равна нулю: , при этом  имеет минимум.

2) Проверка выполнения условий прочности

Максимальное значение изгибающего момента: , а максимальное значение поперечной силы: .

Для одного швеллера № 10: .

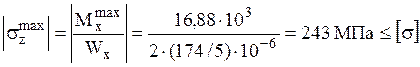=> условие прочности по нормальным напряжениям выполнено.

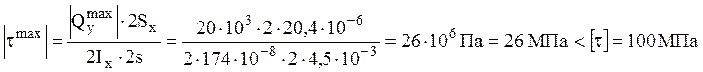
условие прочности по касательным напряжениям выполнено.

5.7 Универсальное уравнение изогнутой оси

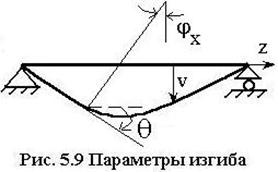Вертикальные перемещения центров тяжестей сечений стержня называется прогибом стержня, а угол между касательной к искривленной оси балки и горизонталью называется углом поворота поперечного сечения (см. рис. 5.9). Функция называется уравнением упругой линией или линией прогибов балки, при этом графически строится изогнутая ось (упругая линия) стержня. Для выбранной системы координат положительным  является перемещение, направленное вниз, а угол  положителен при повороте против часовой стрелки. В рамках технической теории изгиба считаем, что .

Из геометрии следует, что .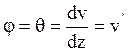

Относительная продольная деформация меняется по высоте сечения по закону: 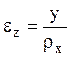, тогда .

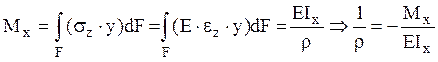Если , то радиус кривизны  и изогнутая ось направлена выпуклостью вниз, если  - выпуклостью вверх.

Точное математическое выражение для кривизны любой плоской кривой 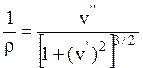 в случае малых изгибных деформаций имеет вид .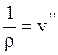

Сравнивая математическое и физическое выражения для кривизн, получим что .

Произведя двойное дифференцирование полученного выражения с учетом дифференциальных зависимостей между внутренними усилиями при изгибе, получим .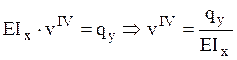

Полагая изгибную жесткость стержня постоянной , выражения для прогибов, изгибающих моментов и поперечных сил получим интегрированием данного выражения:

,

,

,

.

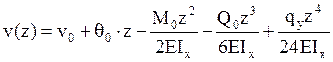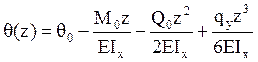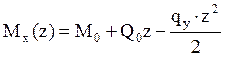В данных выражениях константы интегрирования  определяют прогиб, угол поворота, изгибающий момент и поперечную силу в начале координат. Они называются начальными параметрами.

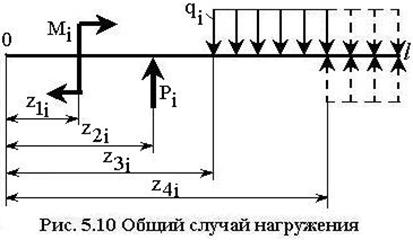
В случае действия произвольного количества нагрузок разного типа (рис. 5.10) полученные выражения можно обобщить

,

,

,

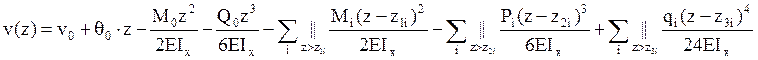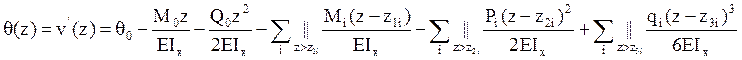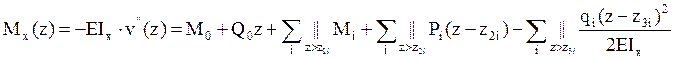Выражение для прогиба называется универсальным уравнением. В данные выражения должны быть включены все нагрузки (внешние и реактивные), действующие на стержень, кроме сосредоточенных нагрузок, действующих на конце стержня, противоположном началу координат. Каждая- нагрузка учитывается в данных выражениях только при превышении осевой координаты указанного значения. В случае если распределенная нагрузка действует только на части длины стержня, то ее необходимо достроить от конца ее действия до конца стержня противоположного началу координат и учесть данное слагаемое в качестве отдельной нагрузки противоположного направления.