Конспект лекционных и практических занятий по дисциплине "Сопротивление материалов", страница 12

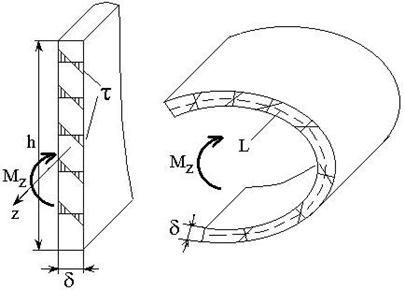
Пусть стержень имеет сечение в виде узкого вытянутого прямоугольника с размерами  где  (рис). Тогда при  получим 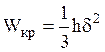, 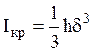. На основании гидродинамической аналогии угол наклона касательной  к поверхности вдоль стороны  практически постоянен. Это означает, что напряжение . Неравномерностью распределения касательных напряжений вдоль узкой стороны пренебрегаем.

Обобщая данные формулы на произвольный тонкостенный профиль, у которого средняя линия имеет длину  и является незамкнутой кривой (рис. 6.3) получим , .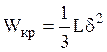

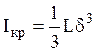При расчете тонкостенных стержней на кручение геометрическая характеристика жесткости обозначается как .

Если сечение состоит из отдельных узких прямоугольников, то 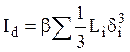 где  - экспериментальный коэффициент, учитывающий некоторое возрастание жесткости сечения за счет областей пересечения прямоугольников и переходных скруглений.

Данный коэффициент принимается равным  (уголок),  (швеллер),  (двутавр).

Относительный угол закручивания определяется формулой 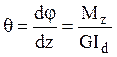, где  - жесткость тонкостенного сечения стержня при свободном кручении.

Для вычисления касательных напряжений  в отдельной -ой пластине стержня представим крутящий момент как сумму моментов, воспринимаемых отдельными частями стержня 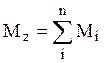. Поскольку угол закручивания  для всех пластин, составляющих сечение, общий, то для каждой -ой пластины . Окончательно, используя выражение для относительного угла закручивания, получим 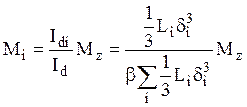 а касательное напряжение равно .

6.3 Свободное кручение тонкостенных стержней замкнутого профиля

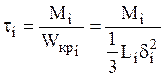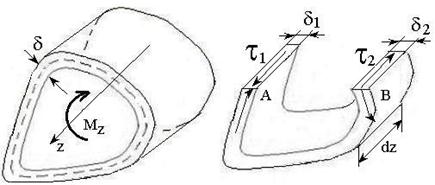
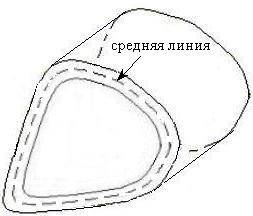Пусть стержень имеет замкнутую форму контура сечения, которое по длине стержня постоянно (рис 6.2). Поверхность, делящая толщину стенки  пополам, называется срединной поверхностью стержня. Линия пересечения срединной поверхности и поперечного сечения называется средней линией тонкостенного поперечного сечения (или его контуром). Вследствие малости толщины контура касательные напряжения  распределены по толщине  равномерно. Толщина стенки  в общем случае является переменной вдоль контура сечения  те . Поскольку боковая поверхность сечения свободна от напряжений, то по закону о парности касательных напряжений, равные им напряжения, направленные по нормали к контуру также отсутствуют. Касательные напряжения действуют только по касательной к контуру. Произведение  называется потоком касательных сил. Поток  имеет размерность  и представляет собой силу, приходящуюся на единицу длины контура.

Для определения связи между касательным напряжением и вызывающим его крутящим моментом рассмотрим равновесие части стержня вырезанной из него поперечными и продольными сечениями, проведенными в произвольных точках  и  контура (рис 63). По закону о парности касательных напряжений в продольных площадках стенки возникают такие же напряжения, как и в поперечном сечении. Проецируя все силы но ось стержня , для данной части стержня получим . Поскольку точки  и  выбраны произвольно то , т.е. при свободном кручении интенсивность потока касательных усилий  вдоль замкнутого контура сечения постоянна для всей длины контура сечения.

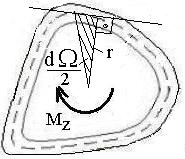
Суммарный момент относительно оси  создаваемый потоком усилий по всему контуру соответствует внутреннему крутящему моменту . В соответствии с рис. 6.4 и  получим  где  - удвоенная площадь сектора в виде элементарного треугольника с основанием ;  - удвоенная площадь, охватываемая контуром сечения.

Окончательно формула для касательных напряжений принимает вид 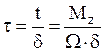 (формула Бредта).

Поскольку при выводе этой формулы использовались только уравнения статики, то задача по определению касательных напряжений при свободном кручении стержня замкнутого одноконтурного сечения является статически-определимой.

В частном случае, для круглого тонкостенного сечения формула для касательных напряжений принимает вид .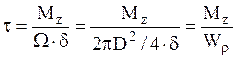

6.4 Жесткость тонкостенных стержней замкнутого профиля при свободном кручении

Для того, чтобы определить угол закручивания  используем равенство , где  - потенциальная энергия деформация элемента длиной ,  - работа моментов , вызвавших деформацию элемента, которой является чистый сдвиг с напряжением . Энергия деформации, сосредоточенная в точке (плотность энергии) при чистом сдвиге будет 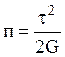, тогда для элемента стержня размером  энергия имеет вид 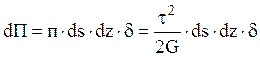. Проинтегрировав по замкнутому контуру  и использовав формулу Бредта, получим значение потенциальной энергии .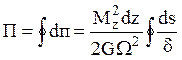

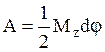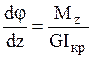Работу момента получим как площадь диаграммы, определяющей связь между крутящим моментом и углом закручивания по закону Гука . Используя равенство , получим , где 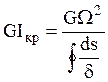 является жесткостью замкнутого сечения при свободном кручении.

В частном случае, жесткость круглого тонкостенного сечения равна .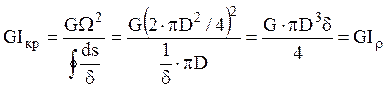

Для замкнутого квадратного сечения, при : .

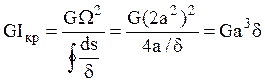Для такого же стержня открытого сечения (если в произвольной стенке имеется разрез), при , получим 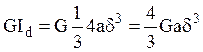 Их отношение .

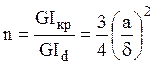Например, при  получим .

Таким образом, при одинаковых условиях углы закручивания замкнутого сечения будут в 300 раз меньше, чем у стержня с прорезью. Также распределения касательных напряжений будут существенно различаться, а деформация открытого профиля будет сопровождаться сильной депланацией.

Пример №1

Сравнить жесткость и прочность открытого и замкнутого круглого тонкостенного профиля при кручении (рис) для

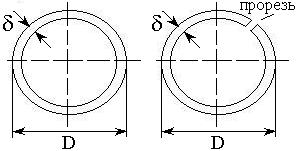Решение

Характеристики жесткости и прочности открытого профиля вычисляется по формулам 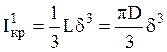 и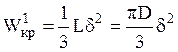

Характеристики жесткости и прочности замкнутого профиля вычисляется по формулам 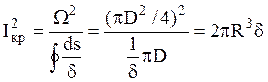 и

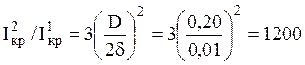Тогда  и

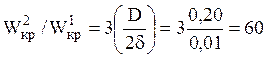
Пример №2

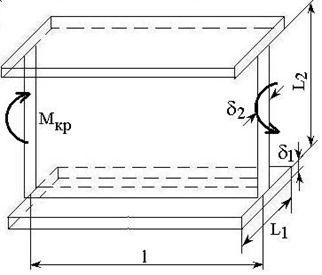Проверить выполнение условия прочности при кручении стержня двутаврового профиля и определить максимальный угол закручивания возникающий при этом

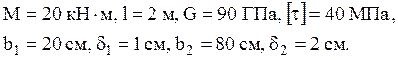
Решение:

Момент сопротивления при кручении стержней открытого профиля определяется по формуле

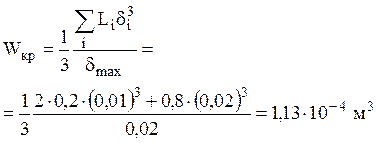
Тогда 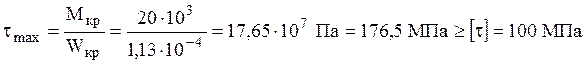 и условие прочности не выполнено.

Геометрическая характеристика жесткости сечения определяется по формуле 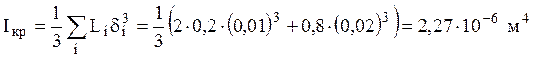, а угол закручивания равен 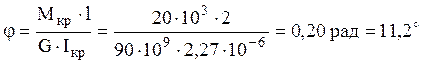. Такое большое значение угла означает плохую работу стержней тонкостенного открытого поперечного сечения на кручение.