Разработка методов многокритериального синтеза сигналов и устройств обработки, обеспечивающих робастные качественные показатели системы, страница 16

Характерной особенностью задачи СВЧ термографии является то, что детектор принимает излучения не только вдоль одного луча, а имеет некоторую диаграмму направленности F(f), поэтому результат каждого измерения представляет собой наложение множества радоновских образов, взвешенных диаграммой направленности в некотором диапазоне углов Df

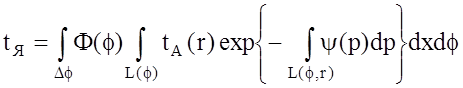.                                    (2.34)

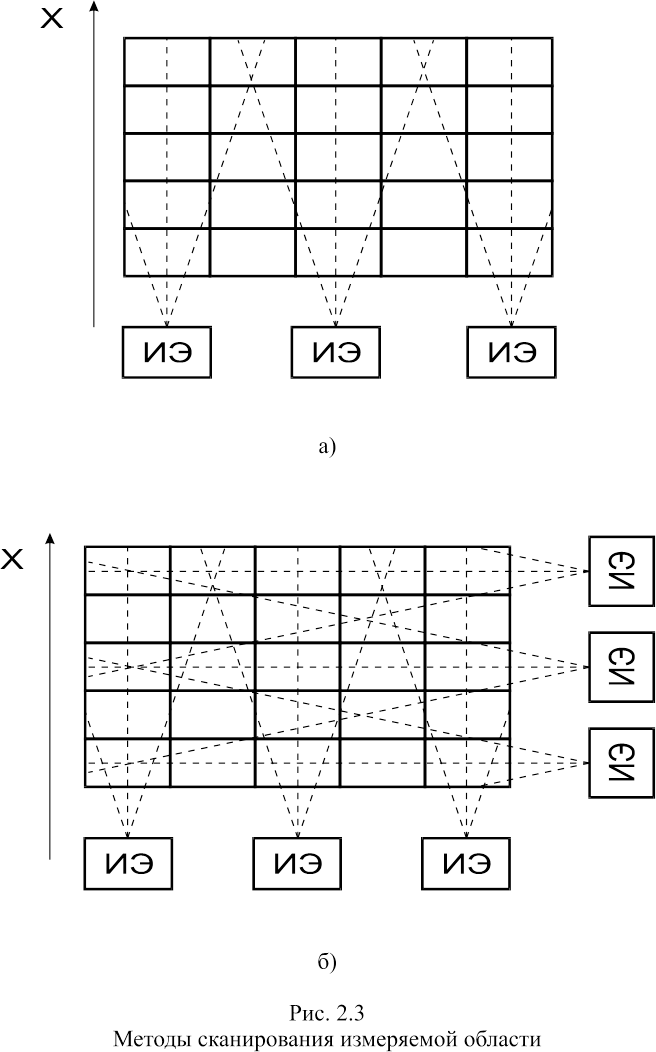
Для решения интегрального уравнения (2.34) воспользуемся алгебраическим методом реконструкции [75, 76]. Для этого разобьем рассматриваемую область на подобласти, в пределах каждой из которых температуру и коэффициент поглощения можно считать постоянными. На границе области расположим измерительные элементы (ИЭ) (рис. 2.3а, 2.3б), которые могут сканировать область под разными углами. Схема сканирования представленная на рис. 2.3б обладает более высокой разрешающей способностью по оси X, чем схема на рис. 2.3а, но применима только при небольших поперечных размерах измеряемой области. Непосредственно сканирование осуществляется либо поворотом ИЭ, либо переключением его антенной системы. При этом количество ИЭ (приемных антенн) и число углов сканирования (т.е. количество необходимых

измерений) зависит от возможностей экспериментатора и особенностей поставленной задачи.

Пусть число ИЭ равно K, и каждый из них в процессе эксперимента сканирует под k углами. Тогда число измерений, произведенное всеми элементами под разными углами, будет K×k = N (всего N лучей). Количество подобластей, на которые разбита рассматриваемая область, равно M. Тогда на основе выражения (2.34) вклад m-й подобласти , через которую проходит n-й луч в измеренную радиояркостную температуру составит

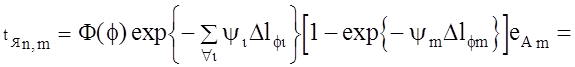
,                     (2.35)

где множитель  определяет поглощение волны, дошедшей до ИЭ от m-й подобласти, i(n,m) - количество участков с различным поглощением fi, через которые проходит n-й луч, Dlfi ‑ расстояние, пройденное n-м лучом в i‑м участке под углом f,  - температура в m-й подобласти, qn,m - коэффициент, отражающий вклад m-й подобласти в измеренную радиояркостную температуру . Аналогично (2.34), суммируя по всем областям радиояркостную температуру, результат n-го измерения получим в виде

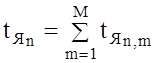.                                                                                       (2.36)

Таким образом, для восстановления глубинного распределения температуры в виде вектора tAнеобходимо решить систему линейных алгебраических уравнений вида:

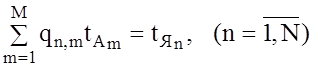.                                                             (2.37)

Система (2.37) состоит из N уравнений и содержит M неизвестных. Правая часть системы представляет собой результаты измерений и в общем случае задана с некоторой погрешностью dЯ.

Поскольку в общем случае M ¹ N, то полученную систему можно решать различными способами: например обобщенным методом наименьших квадратов и методом регуляризации [55]. Решение задачи методом наименьших квадратов находится из решения матричного уравнения:

Q*QtA = Q*tЯ,                                                                                         (2.38)

где Q - матрица, состоящая из коэффициентов qn,m, Q*- матрица, эрмитово сопряженная матрице Q (т.к. коэффициенты qn,m ‑ действительные числа, то матрицаQ просто транспонированная по отношению к матрице Q), tA- искомый вектор температур, tЯ- вектор радиояркостных температур. Однако на практике матрица Q плохо обусловлена [55] и, следовательно, вектор искомого решения tA сильно зависит от точности задания исходных данных. Иными словами, даже небольшие погрешности измерения радиояркостной температуры ведут к значительным искажениям решения. Сделать искомое решение более устойчивым позволяет использование метода регуляризации по Тихонову [28] со стабилизатором нулевого порядка, при котором решение задачи ищется из уравнения:

(Q*Q + aJ) tA = Q* tЯ,                                                                           (2.39)

где матрица Q состоит из коэффициентов qm,n, tA- искомый вектор температур, J - единичная матрица, a - параметр регуляризации.

В то же время известно [63], что практические распределения температуры являются гладкими функциями и, как показано в [79], в данном случае более целесообразно использование стабилизатора первого порядка, при котором решение задачи ищется из уравнения вида

(Q*Q + a(V4J + V5F2)) tA = Q* tЯ,                                                          (2.40)

где V4 и V5 - весовые коэффициенты.

Для проверки эффективности работы данных методов был проведен численный эксперимент [79,…, 84]. В процессе эксперимента по заданному вектору tA0 был найден теоретический вектор радиояркостных tЯ0 температур на который затем накладывалась аддитивная помеха, учитывающая неточность измерения tЯ= tЯ0 + e(e - вектор ошибок измерения). По полученному в результате вектору радиояркостных температур tЯ проводилось восстановление глубинного распределения температуры с помощью алгоритмов (2.38), (2.39) и (2.40). На рис. 2.4.а приводится исходное распределение температуры tA0 (чем выше температура, тем светлее изображение; стрелкой показано направление сканирования), а на рис. 2.4б, 2.4в и 2.4г результаты, полученные при использовании методов (2.38), (2.39) и (2.40) соответственно. Видно, что из-за плохой обусловленности матрицы Q метод наименьших квадратов не позволяет восстановить глубинное распределение температуры. Сравнение формы полученных темпера-

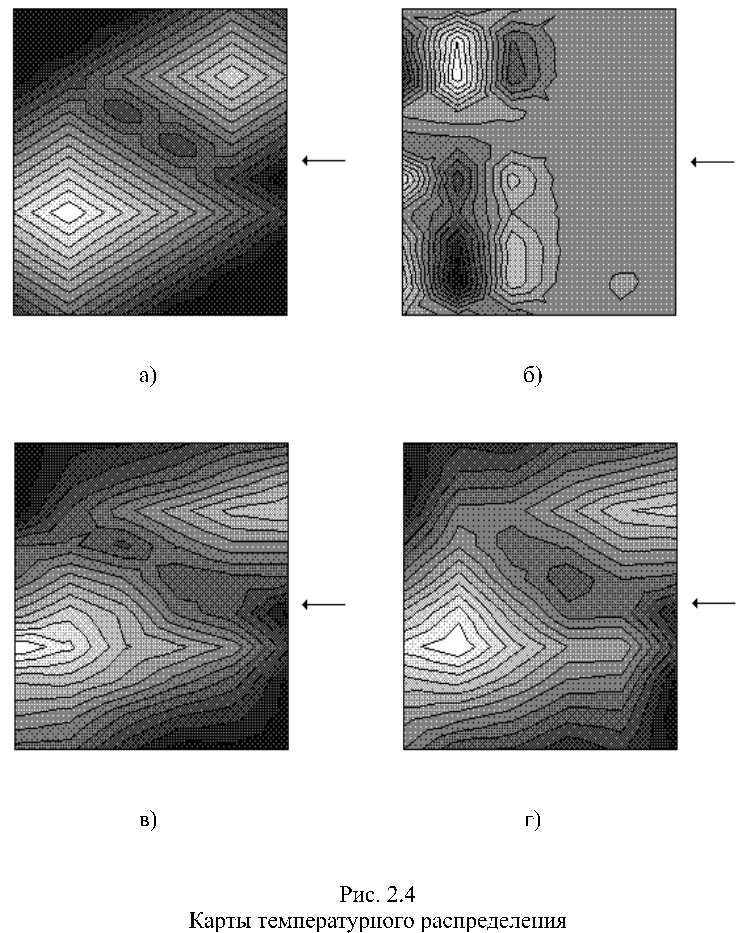
турных распределений показывает, что решение tAP полученное по методу (2.40) (при V4 = 0.1 и V5 = 0.9) дает более высокую точность восстанов-

ления и разрешающую способность по сравнению решением tAH, полученным по методу (2.38). При этом выигрыш в точности составляет:

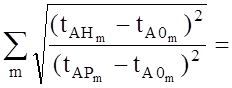1.548 .