Теория автоматического управления как математическая теория информационных процессов передачи и преобразования сигналов, страница 8

6.АЧХ

АЧХ представляет собой по амплитуде единичное звено.

7.ФЧХ

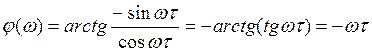
Сдвиг по фазе тем больше, чем больше частота и задержка τ (τ=const)

8.ЛАЧХ

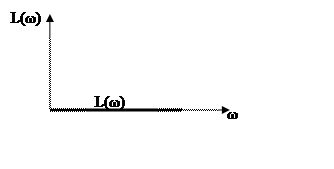
9.ЛФЧХ

 

10.Годограф

                         

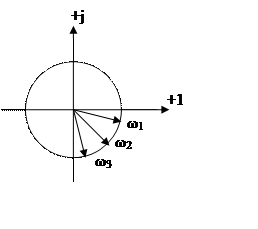
Все остальные звенья сводятся к изученным семи звеньям. Но существует форсирующее звено второго порядка, которое нельзя свести к изученным.

 

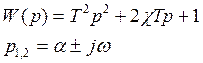
Но в технике данное звено почти не используется.

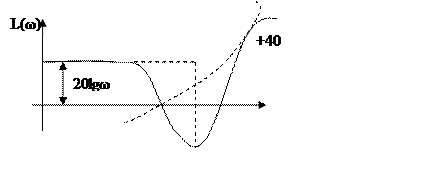ЛАЧХ такого звена имеет вид

Это звено сильно увеличивает высокочастотные помехи. Оно может использоваться в качестве фильтра, так как гасит некоторые частоты.

4.Устойчивость линейных САУ

4.1 Вводный пример, характеризующий изучаемую проблему.

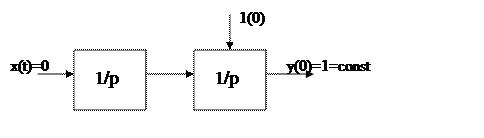Возьмем два звена, которые являются устойчивыми, и запустим их на моделирование.

Если мы попытаемся эту структуру соединить обратной связью

 

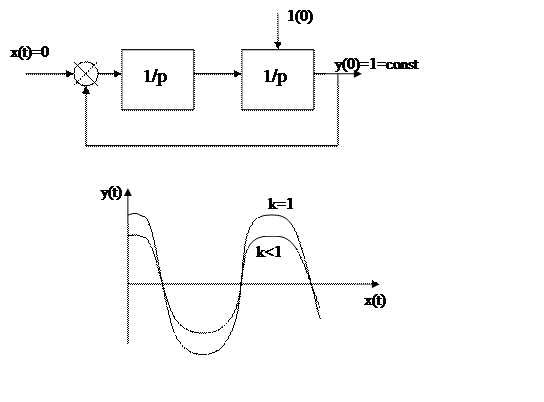k<1 – затухание, значит система станет неустойчивой.

Впервые термин «устойчивость» ввел А.Н. Крылов (изучал качку кораблей).

4.2 Формализованное понятие устойчивости

Все линейные звенья описываются уравнением (*) и это уравнение связывает входные и выходные сигналы  и их производные.

Общее решение уравнения (*) будет выглядеть следующим образом

                                                      

y(t)=y_{частное неоднород. диф. ур-я}(t)+y_{общее однород. диф.ур-я}(t)

Однородное дифференциальное уравнение – это исходное уравнение (*) с нулевой правой частью.

По этой причине y_общ(t) описывает поведение системы под действиями внутренних причин, которые представлены ненулевыми начальными условиями (зарядом конденсатора, сжатой пружиной, ненулевой скоростью инерциальных масс)

Частное решение (y_{частное}) описывает вынужденное движение системы под действием входного сигнала при конкретном виде возмущения.

y_{частное} зависит от вида входного сигнала.

Нас интересует y_общ , поэтому y_общ в теории управления принято называть свободной составляющей процесса или переходным процессом.

Устойчивым движением системы будем называть  такое движение, когда

Система устойчива, если у_{свобод.} с течением времени затухает, то есть по амплитуде стремится к нулю.

4.3 Общие условия устойчивости для линейных систем

Приведем формализованное требование к коэффициентам уравнения (*), которое вытекает из условия устойчивости.

Однородное дифференциальное уравнение в операторном виде выглядит следующим образом

    (1)

Известно, что свободное решение, то есть решение дифференциального уравнения (1) может быть найдено

где C_1....C_n – постоянные интегрирования, зависящие от начальных условий на выходной координате y(t) и ее производной.

δ_1…δ_n – корни характеристического уравнения.

Это характеристическое уравнение образовано коэффициентами уравнения (1).

     (***)

По теореме Безу известно, что уравнение (***) имеет n корней, где n – порядок характеристического уравнения, порядок уравнения (*), поэтому эту величину называют порядком системы.

Поскольку коэффициенты уравнения (***) все действительные, то корни δ_к либо действительные, либо комплексносопряженные.

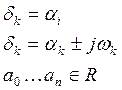
Таким образом можно сказать будет ли сходиться к нулю У_{свобод.}, если мы умеем составлять уравнение (1) и можем найти  δ_к.

Рассмотрим компоненты У_свобод, их вид зависит от корней характеристического уравнения.

 

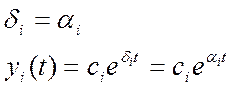
График показывает природу неустойчивости.

Можно утверждать, что система устойчива, если все α_i<0 и принимают значения от 1 до n.

Если найдется хотя бы 1 корень характеристического уравнения, это приведет к тому, что У_свобод =∞.

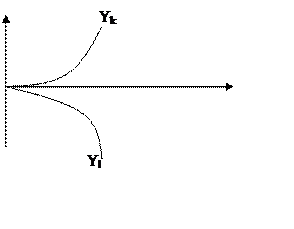НО:  Рассмотрим действительные корни. Может существовать вырожденный случай, когда два корня компенсируют друг друга.

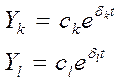
Это жесткие системы автоматического управления, которые могут существовать, но ограниченное время.

Из-за неизбежного расхождения параметров системы рано или поздно одно из компонент забегает вперед, а вторая отстает.

Такая система применяется в военной промышленности.

Плюсом такой системы является высокая управляемость и малое потребление ресурсов.

Таким образом, при действительных корнях характеристического уравнения система устойчива тогда и только тогда, когда все корни находятся в левой полуплоскости, т.е. действительная часть меньше нуля.

Рассмотрим более общий случай комплексно-сопряженных корней.

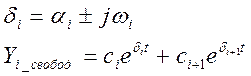
Мнимые части по формуле Эйлера должны уничтожиться в силу комплексно-сопряженного характера.

Вид кривой определяется коэффициентом α_i

 

График характеризует устойчивую систему.

Если α_i>0, тогда график имеет вид

График характеризует неустойчивую систему.

Система устойчива тогда и только тогда, когда корни характеристического уравнения находятся в левой полуплоскости.

Для комплексно-сопряженных корней, верно, то же утверждение, что и для действительных корней.

 Если корень характеристического уравнения находится в правой полуплоскости, тогда система является неустойчивой.

Характеристическое уравнение подразумевается для замкнутой системы.

4.4 Алгебраические критерии устойчивости

Алгебраические критерии устойчивости сформировались из-за необходимости решения характеристического уравнения.

Если корни находятся на границе, т.е.

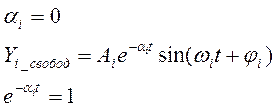
Поэтому процесс будет выглядеть как незатухающая синусоида.

 

С математической точки зрения система устойчива, но практическая сторона этой системы говорит о том, что устойчивости нет. Система находится на грани устойчивости и практически не работоспособна.

Прямого решения характеристического уравнения для систем 4 и выше порядка не существует.

4.4.1 Алгебраический критерий Гурвица

Для системы составляется ряд определителей. Главный определитель, называемый определителем Гурвица, имеет вид матрицы с n столбцами и n строками.

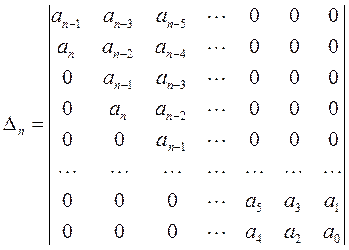
Выделим в главном определителе диагональные миноры, т.е. определители, соответствующие элементам главной диагонали.

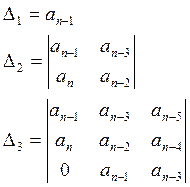
Таких миноров можно найти Δ_n-1

Сформулируем критерий Гурвица

Для устойчивости системы необходимо и достаточно, чтобы все определители Гурвица были больше нуля при a_n>0

Δ_n>0, Δ_n-1>0... Δ₁>0

Примеры: