Теория автоматического управления как математическая теория информационных процессов передачи и преобразования сигналов, страница 5

     

 

полином

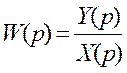
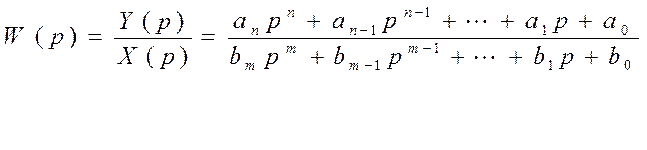
Множество корней полинома представляется дробно-рациональным уравнением

Теорема Безу

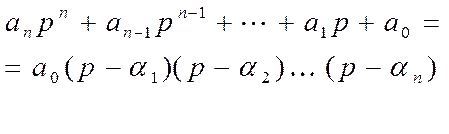
α_1,…α_n – корни полинома

p=α_ii=1…n

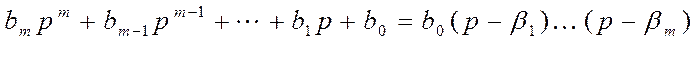
β_1,β_m- нули передаточной функции

α_1, α_n – полюса передаточной функции

2.5 Временные характеристики линейных звеньев

Для изучения свойств элементарных звеньев удобно использовать типовые воздействия.

По характеру отклика на эти воздействия мы можем судить о их динамических свойствах.

Переходная функция (h(t))

Переходной функцией системы (звена) называют функцию, описывающую изменение выходной величины системы (звена), когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях.

Иными словами переходная функция – реакция звена на входной сигнал вида единичной ступенчатой функции.

Аналитически выражение единичного ступенчатого воздействия  можно описать единичной функцией:

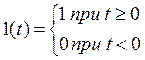
Представим данное звено графически

Y(t) = h(t)

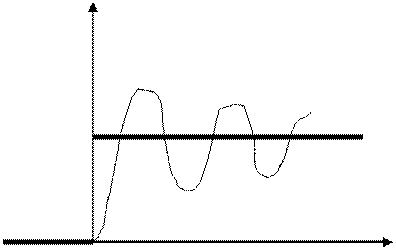
График переходной функции – кривая зависимости функции h(t) от времени t – называют переходной характеристикой.

h(t)

		t=0		t

1

X(t)

h(t)

Свяжем переходную функцию с передаточной функцией.

       

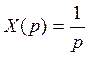
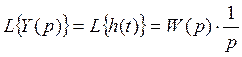
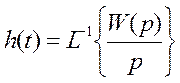
Пример:

Рассмотрим двигатель постоянного тока, ротор такого двигателя имеет следующий вид

I

M

                                                                                

ω

                                                                                

Передаточная функция такого звена будет выглядеть

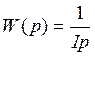
M(t)=1(t)

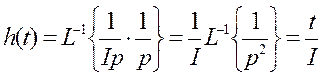
ω=t/I (M=1)

                                              

                              

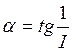
Весовая функция (w(t))

Под весовой функцией будем понимать реакцию системы на типовое воздействие типа δ импульса при нулевых начальных условиях.

График весовой функции называют импульсной переходной характеристикой.

Физически единичный импульс можно представить как очень узкий импульс, ограничивающий единичную площадь. Математически он описывает функцией , которую называют дельта-функцией.

 

Необходимо установить связь между передаточной и весовой функцией

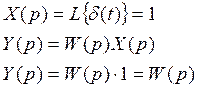
Таким образом, изображение весовой функции равно передаточной функции.

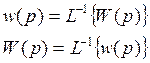
Приведем пример.

Рассмотрим ротор двигателя постоянного тока. Его передаточная функция будет иметь вид

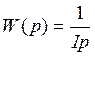
M(t)=δ(t)

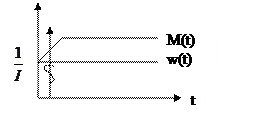
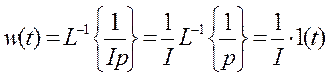
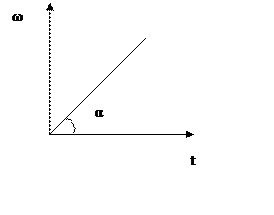
Статическая характеристика линейных звеньев

Статическая характеристика линейных звеньев – это зависимость между установившимися значениями входного и выходного сигнала.

Yуст(t)=ƒ(Xуст)

 

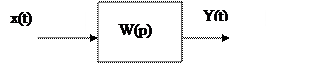  k=tg α, где k- коэффициент передачи      (усиления)

Пользуясь теоремой о конечном значении, свяжем передаточную функцию и коэффициент передачи (усиления).

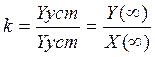
Y(∞)=kX(∞)

Y(0)=kX(0)-теорема о конечном значении

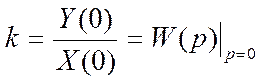
Частотные характеристики звеньев

Предположим, что к звену приложено синусоидальное входное воздействие.

 

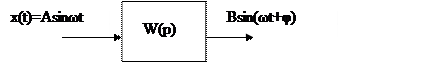φ-фазовый сдвиг.

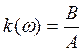
k(ω)-коэффициент передачи амплитуды φ(ω)

 

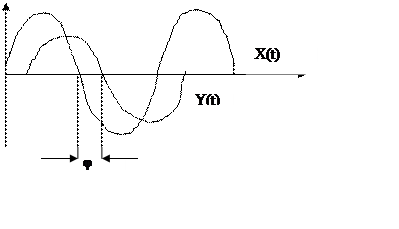Эксперимент по прохождению гармонического сигнала представляет нам две характеристики объекта – АЧХ (амплитудно-частотную характеристику k(ω)) и ФЧХ (фаза - частотную характеристику φ(ω)).

Удобно ввести комплекснозначную частотную характеристику, которая содержала бы всю информацию об объекте, т.е. объединила АЧХ и ФЧХ.

Ф(jω)-частотная характеристика (ЧХ)

Для введения ЧХ будем полагать, что на входе действует обобщенный гармонический сигнал .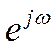

 

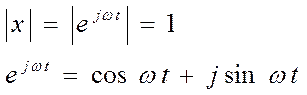
  ω=var

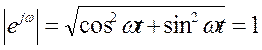
Преобразуем уравнение (*) следующим образом:

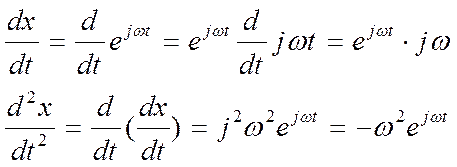
Таким образом мы находим все производные, тогда производная n-ного порядка будет иметь следующий вид.

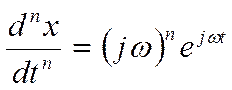
-входной сигнал.

Аналогичным образом будут выражаться производные для выходного сигнала:

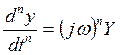
Определим частотную характеристику как отношение выходного сигнала к входному, с учетом уравнения (*)

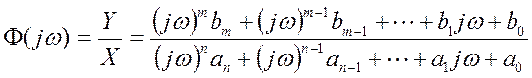
Сравним полученную частотную характеристику с передаточной функцией

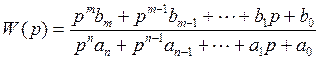
При сравнении видно, что из передаточной функции путем замены p на jω можно получить частотную характеристику.

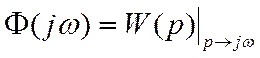
Свяжем ЧХ с АЧХ и ФЧХ

P(ω)-вещественная частотная характеристика (ВЧХ)

Q(ω)-мнимая частотная характеристика (МЧХ)

АЧХ будет иметь следующий вид:

А ФЧХ найдется по формуле:

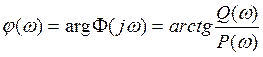
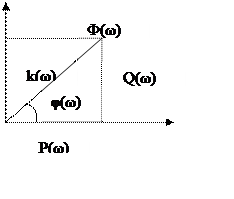
Графически ФЧХ и АЧХ будут выглядеть так:

	+j

 

+1

                                                      

ω –является переменной величиной

ω=0…∞

При этом конец радиус-вектора комплекснозначной характеристики Ф(jω) будет прочерчивать на плоскости кривую.

Геометрическое место точек конца вектора Ф(jω) при изменении частоты ω=0…∞ будет называться годографом Найквиста.

2.6   Логарифмические амплитудно-частотные характеристики и логарифмические фазочастотные характеристики как инструмент инженерного проектирования

Предположим, что нам известны АЧХ и ФЧХ для некоторого элементарного звена.

 

                                                                                                     ω

k(ω)

                                           ω      φ(ω)

Перестроим эти характеристики в логарифмическом масштабе.

Назовем логарифмической амплитудно-частотной характеристикой (ЛАЧХ) зависимость следующего вида: