и(х, 0) = φ(х), ut(х, 0) = y(х) (х = x1,…, xп).
В качестве граничных условий мы будем рассматривать линейные относительно функции и(х, t) граничные условия вида
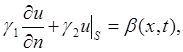
где производная берётся по направлению внешней нормали, g1, g2, b - заданные на S непрерывные функции. Для стационарных задач функция b не зависит от t. Если b(x, t) = 0, то граничные условия называют однородными. Очевидно, что |g1| + |g2| ≠ 0, причем мы будем считать, что
![]()
![]()
Граничные условия такого вида встречаются наиболее часто. Для них принята следующая терминология:
a) g1 = 0 - граничные условия 1-го рода (соответственно первая краевая задача);
b) g2 = 0 - граничные условия 2-го рода (вторая краевая задача);
c) g1 ≠ 0, g2 ≠ 0 - граничные условия 3-го рода (третья краевая задача).
Для стационарных процессов колебаний и диффузии, описываемых эллиптическими уравнениями вида (1с)
Lu = – F(x), (1)
некоторые краевые задачи имеют специальные названия.
Если в операторе L имеем k(x) = const, q(x) = 0, то уравнение (1) принимает вид уравнения Пуассона
Du = – f (2)
(при f = 0 мы получаем уравнение Лапласа).
Первая краевая задача для уравнений Лапласа и Пуассона называется задачей Дирихле:
Du = – f, ![]()
Вторая краевая задача называется задачей Неймана:
Du = – f, 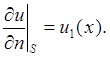
(Вопросы, связанные с гладкостью решений, формой областей и гладкостью дополнительных данных, будут обсуждаться позднее при решении конкретных задач.)
Замечание 1. Эллиптические уравнения могут описывать не только стационарные процессы, но и установившийся режим. Пусть в волновом уравнении
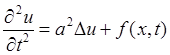
внешнее возмущение f(x, t) - периодическое, с частотой w и амплитудой f0(x), т.е.
![]()
Если искать периодическое решение и(х, t) с той же частотой и неизвестной амплитудой u0(х) в виде
![]()
(за счет диссипативных процессов при больших t начальные возмущения в реальных системах затухают и решение выходит на режим внешнего воздействия), то для функции u0(х) получим эллиптическое уравнение
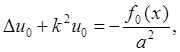
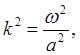
которое называется уравнением Гельмгольца.
Замечание 2. Специальным видом граничных условий можно считать условия сопряжения на границе двух сред.
a) Для уравнения теплопроводности на границе двух областей, не содержащей источников, должны быть равны температуры и потоки тепла:
![]()
![]()
b) В задаче Стефана (например, задача о промерзании среды) условия сопряжения ставятся на движущейся границе, где и = 0. См. также условия Гюгонио на фронте ударной волны [1].
c) Другим интересным примером являются условия сопряжения в точке приложения силы F(t), движущейся вдоль бесконечной струны со скоростью v0 (сила приложена в точке x0 = v0t).
Поставим задачу Коши:
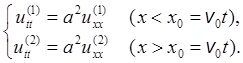
Начальные условия:
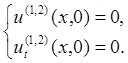
Найдем условия сопряжения в точке х = x0. Пусть в момент t = t1 сила была приложена в т. х = х1 и в т. х = х2 при t = t2 (Рис. 8).
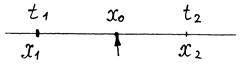
Рис. 8
![]()
![]()
![]()
1) Условие непрерывности струны:
![]()
2) Второе условие найдём, используя второй закон Ньютона:
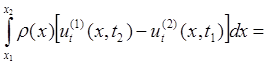
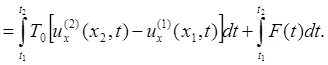
Для выражений в квадратных скобках формулу Лагранжа для конечных приращений нельзя применять, так как эти функции имеют разрыв производной (Рис. 9, 10). Но теорему о среднем к интегралам применять можно:
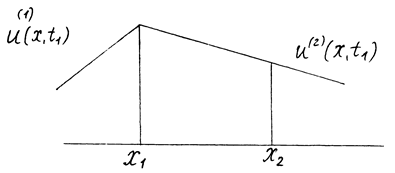
Рис. 9
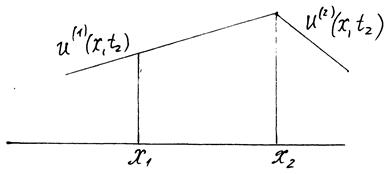
Рис. 10
![]()
![]()
После деления на Dt и предельного перехода Dx → 0, Dt → 0, получим:
– rv0{ut} = Т0{ux} + F(t), где {f} = f(x0 + 0) – f(x0 – 0). Величину {ut} можно выразить через {ux}. Так как условие непрерывности струны выполняется при любых t, то дифференцируя по t при х = x0 = v0t первое условие сопряжения, получим
![]()
откуда
![]()
В результате получаем следующую связь производных ux(x, t) в точке х = x0:
![]()
Отсюда ![]() так
как
так
как ![]()
При v0
= 0 получаем ![]() что совпадает с результатом
сложения сил в точке х = 0 (Рис. 11):
что совпадает с результатом
сложения сил в точке х = 0 (Рис. 11):
![]()
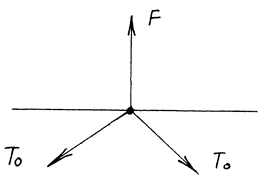
Рис. 11
3. Роль характеристик в постановке краевых задач.
Прежде чем переходить к методам решения рассмотренных выше задач, обратимся ещё раз к уравнению в частных производных второго порядка с двумя независимыми переменными
![]() (3)
(3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.