Методы математической физики: Курс лекций (Вывод основных уравнений математической физики. Метод функций Грина. Единственность решения основных задач), страница 12

При n = 1 имеем обыкновенное дифференциальное уравнение. Покажем, что при п = 2 интересующее нас приведение к каноническому виду всегда можно выполнить. В этом случае имеем

                                         (1a)

Будем исходить из общей формулы

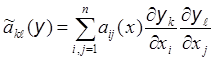
                                                 (1)

В силу (1)

                                                        (2)

                                                        (3)

                                               (4)

Для сокращения письма удобно ввести новые обозначения: a₁₁ = a, a₁₂ = b, a₂₂ = с. Тогда равенства (2) - (4) запишутся в виде

                                                             (5)

                                                             (6)

                                                   (7)

Очевидно, что коэффициенты а, b, с не могут одновременно обращаться в нуль, т.е. |a| + |b| + |c| > 0. Это требование эквивалентно требованию a ≠ 0. В самом деле, если при а = 0 имеем с ≠ 0, то достаточно поменять местами х и y. Если же при a = 0 имеем с = 0, b ≠ 0, то достаточно произвести замену х' = х + y, y' = х – y. Тогда ã₁₁ = ã₂₂ ≠ 0.

Оказывается, что тип уравнения (1а) определяется знаком выражения D = – a₁₁a₂₂ = b² – ac:

D > 0 - гиперболический тип,

D = 0 - параболический тип,

D < 0 - эллиптический тип.

Из формул (5) и (7) следует, что

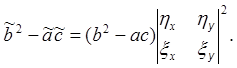
Докажем это утверждение и заодно приведём к каноническому виду уравнение (1а) в каждом из трёх случаев.

Попробуем выбрать таким образом переменные x и h, чтобы ã = 0, = 0. Из условия ã = 0 имеем

 

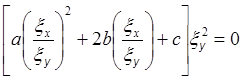
или

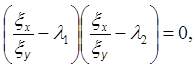                                                             (8)

где

 

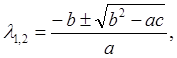
1) Изучим сначала случай b² – ас > 0, когда функции l₁(х, y) и l₂(х, y) вещественны и l₁ ≠ l₂. Пусть x_x/x_y = l₁, т.е. x_x – l₁x_y = 0. Если рассмотреть линии уровня некоторой функции x = x(x, y) двух переменных, т.е. координатные линии x(x, y) = C, вдоль которых новая независимая переменная x постоянна, то выражение x_x – l₁x_y = 0 можно рассматривать как производную функции x(x, y) по х вдоль таких линий y = y(х, С), для которых

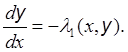
Пример.  (см. С.К. Годунов, Уравнения математической физики, М., Наука, 1979, гл. 1, §5).

Таким образом, если x(x, y) = C есть общий интеграл уравнения , то замена x = x(x, y) обратит в нуль коэффициент ã. Аналогично из условия , т.е.

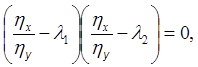
можно найти семейство h(x, y) = C как общий интеграл уравнения  (условие  мы уже фактически использовали). Функции x = x(x, y), h = h(x, y) называют характеристиками уравнения (1а).

В результате перехода к новым независимым переменным уравнение (1а) примет вид

где

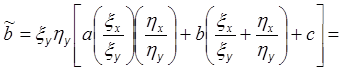
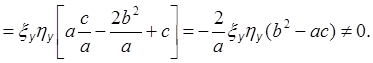
Канонический вид:

Другой канонический вид:

    

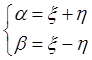
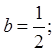
Мы получили уравнение гиперболического типа.

2) Пусть b² – ac = 0, l₁ = l₂ = , x(x, y) = с есть общий интеграл уравнения . Пусть x = x(x, y), h = x (в качестве h(x, y) можно взять любую функцию). Покажем, что такая замена возможна:

 

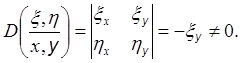
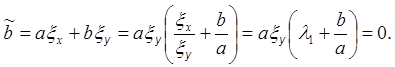
Канонический вид: u_hh +  = 0.

3) b² – ас < 0, : x_x – l₁x_y =0,   (чертой обозначен знак комплексного сопряжения).

Если подойти к комплексным характеристикам, как к вещественным (то есть формально считать, что они существуют), то можно положить

x = a + ib, h = a – ib.

При этом условие ã = 0 даёт

откуда, приравнивая нулю вещественную и мнимую часть, получим

Отсюда видно, что если бы мы перешли от x, y сразу к a, b, то получили бы (см. формулы (5) - (7)) уравнение

или

так как ã ≠ 0 (соответствующий квадратный трёхчлен имеет комплексные корни).

Ниже (см. §3) будет показано, что характеристики играют важную роль при постановке задач математической физики.

§3. Постановка основных краевых задач математической физики

1. Выбор функции, вывод уравнения, задание дополнительных условий (начальных и граничных).

Чтобы полностью описать тот или иной физический процесс, необходимо, прежде всего, выбрать функцию, характеризующую его, и составить для неё уравнение. Заметим, что интересующая нас функция не должна быть обязательно вещественной. Уравнения, выражающие закон природы, могут иметь наиболее простой вид, когда они записываются для комплексных функций, которые лишь после некоторых математических действий над ними дают непосредственно наблюдаемые величины: уравнение Шредингера записывается для волновой функции y, а наблюдаемой величиной является, например, yy^* - так называемая плотность вероятности.