Математика \ Математическое моделирование на ЭВМ

Линейное программирование. Задача линейного программирования (ЗЛП), страница 3

Примеры крайних точек. Для отрезка - это концы отрезка. Для объема шара это – поверхность шара. Для многоугольника – это его углы.

В дальнейшем нам понадобится следующее свойство выпуклых множеств. Пересечение любого числа выпуклых множеств является выпуклым множеством.

Пример. Пересечением отрезков [1; 4] и [2; 8] является отрезок [2;4].

Свойства планов ЗЛП.

Основные свойства планов задачи линейного программирования изложим в виде шести теорем.

1. Множество планов ЗЛП , удовлетворяющих неравенство

(или в векторной записи - ax£ b₁), является выпуклым.

Действительно, пусть х¢ и х² планы, удовлетворяющие указанное неравенство. То есть, ax¢£ b₁ и ax²£ b₁.

Построим выпуклую линейную комбинацию l₁х¢+l₂х². Получим

Видим, что выпуклая линейная комбинация - тоже план, удовлетворяющий, указанное неравенство. Теорема доказана.

2. Множество планов ЗЛП – выпуклое.

Множество планов, удовлетворяющих систему ограничений

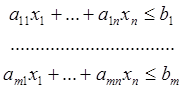
представляет собой пересечение множеств, удовлетворяющих каждое неравенство в отдельности. А пересечение выпуклых множеств является выпуклым. Что и требовалось доказать.

3. Если система векторов содержит m линейно-независимых векторов: , то существует допустимый план вида

0;…0) (1)

и является единственным планом такого вида.

Рассмотрим систему уравнений (векторная запись)

(2)

Поскольку n > m, система уравнений (2) имеет бесконечно много решений.

Запишем ее так

(3)

В левой части равенства оставлены независимые . Тем х_i (i = m+1, m+2, …, n), что расположились справа, присвоим значение 0. Получим m независимых уравнений с m неизвестными. Новая система уравнений будет иметь единственное решение для . При этом остальные х_i = 0. Теорема 3 – доказана.

В дальнейшем систему независимых векторов будем называть базисом, переменные - базисными переменными, остальные переменные - - свободными переменными. Если свободные переменные равны нулю, а остальные неотрицательны, то такое частное решение задачи называется опорным планом.

4. Допустимый план вида является крайней точкой многогранника планов.

Допустим, что х – не крайняя точка. Тогда ее можно представить как выпуклую линейную комбинацию крайних точек: , где х¢ и х² - крайние точки. Последние n-m элементов точки х равны нулю только в том случае, если они равны нулю в точках х¢ и х². Следовательно, точки х¢ и х² имеют один и тот же вид: и .

Но согласно теореме 3 план подобного вида существует только один. Значит, точки х, х¢ и х² это все одна и та же точка, которая не может быть выражена как выпуклая линейная комбинация других точек. Значит, х является крайней точкой.

5. Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной крайней точке многогранника решений.

Пусть целевая функция принимает экстремальное значение в точке х*, то есть при поиске максимума , где z – целевая функция. И пусть точка х* не крайняя. Тогда ее можно представить как выпуклую линейную комбинацию крайних (угловых) точек х¢, х², …, х⁽^k⁾:

Тогда целевую функцию можем представить так

Обозначим наибольшее буквойM. То есть, . Тогда . Значит, , то есть максимум целевой функции равен М. Следовательно, достигается в той крайней точке, где .

6. Если целевая функция достигает экстремума более чем в одной крайней точке, то она достигает того же экстремума в любой точке, являющейся их выпуклой линейной комбинацией.

Пусть максимальна в точках