Линейное программирование. Задача линейного программирования (ЗЛП), страница 2

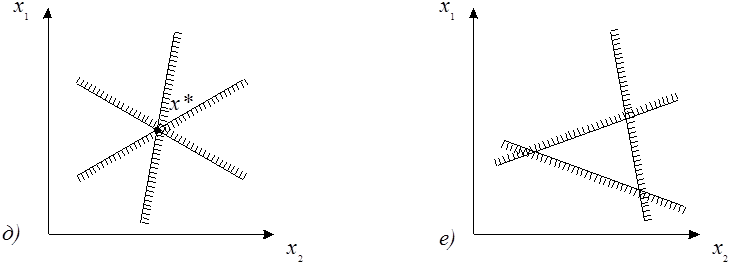
5.3. Графическое решение задачи линейного программирования

В настоящее время вследствие распространения персональных компьютеров и программного обеспечения графическое решение задачи линейного программирования практического значения не имеет. Кроме того, графическое решение задачи линейного программирования возможно лишь при числе переменных, равном 2.

Поэтому ограничимся кратким перечислением порядка действий при графическом решении задачи.

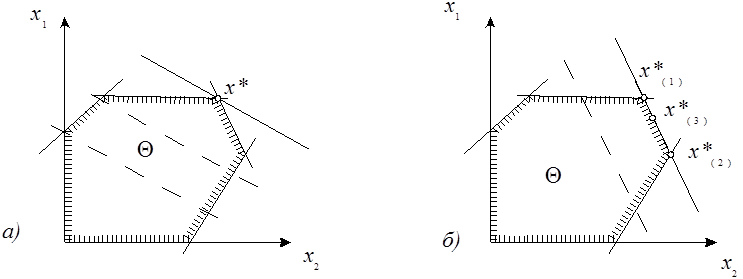
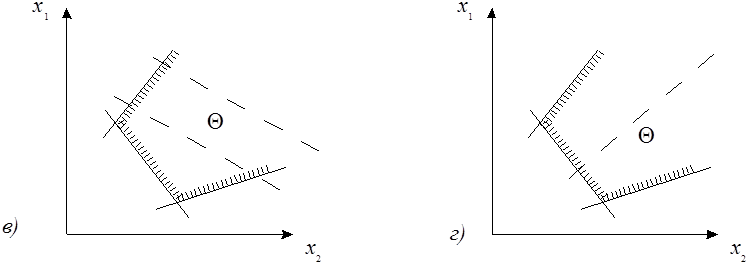
1.  Используя систему ограничений построить область допустимых планов (решений).

2.  Построить вектор С – градиент.

3.  Провести произвольную линию уровня, перпендикулярную градиенту.

4.  Переместить линию уровня в направлении вектора С так, чтобы она касалась области допустимых решений в ее крайней точке. При поиске минимума – перемещение выполнять в крайнюю  в направлении антиградиента точку.

5.  Координаты  крайней точки и есть оптимальный план.

Экстремум целевой функции равен , где  с₁ и с₂ – коэффициенты целевой функции.

5.4. Геометрическая интерпретация задачи линейного программирования (ЗЛП) с n переменными

При числе переменных n задача имеет вид:

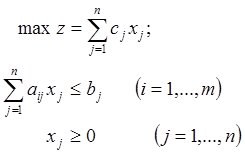
Переменные образуют n-мерное пространство. Каждое уравнение

 

представляет собой гиперплоскость, разрезающую пространство на две части: в первой части  > b_i, во второй -  < b_i.

Во второй половине гиперплоскости расположены допустимые планы. Всеми неравенствами ограничена часть n – мерного пространства – область допустимых решений.

В n-мерном пространстве область допустимых решений представляет собой многогранник планов. Каждая вершина многогранника n-мерная точка – место пересечения m гиперплоскостей. По аналогии с двухмерным случаем, можем предполагать, что по крайней мере одна из вершин многогранника планов и является точкой оптимального плана.

5.5. Формы записи задачи линейного программирования

Общая задача линейного программирования имеет вид:

Целевая функция -

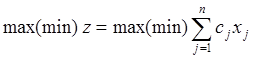
ограничения -

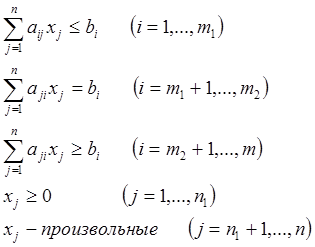
Общая задача охватывает все возможные варианты. При организации решения задачи от общего вида переходят к канонической форме записи ЗЛП.

Каноническая форма записи задачи линейного программирования имеет вид:

Целевая функция -

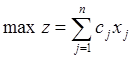
ограничения -

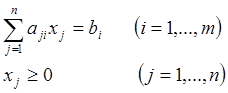
При этом все b_i положительны.

Матричный вид записи канонической формы ЗЛП получим, введя обозначения:

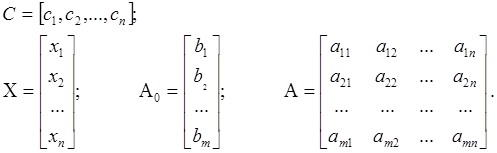
При этом запись канонической формы ЗЛП приобретает вид:

max z = CX

AX = A₀

X ³ 0

Векторный вид записи канонической формы ЗЛП получим, введя обозначения:

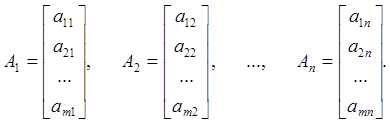
При этом запись канонической формы ЗЛП приобретает вид:

max z = CX

A₁x₁ + A₂x₂ + … +A_nx_n = A₀

X ³ 0

Отметим связь между элементами матричной и векторной записей: A = [A₁  A₂ … A_n].

5.6. Свойства решений задачи линейного программирования

Понятие о выпуклом пространстве (множестве).

Пространство (множество) называется выпуклым, если вместе с его точками х₁ и х₂ содержит все точки отрезка , то есть точки . При этом точки x представляют собой выпуклые линейные комбинации точек х₁ и х₂.

Другой вид записи выпуклой линейной комбинации: ,  где    .

Возможна выпуклая линейная комбинация не двух, а большего числа точек. Тогда 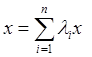, причем 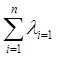, где n – число точек.

Примеры выпуклых пространств.

Точки, расположенные на отрезке прямой, образуют выпуклое линейное пространство. Рассмотрим, например, отрезок [2; 4]. Лежащая между точками 2 и 4 точка 3 (как и любая другая) может быть представлена как их выпуклая линейная комбинация: 3 = (1/2)2 + (1/2)4.

Множество точек внутри шара образует выпуклое линейное пространство. Каждая такая точка может быть представлена как точка, лежащая на отрезке, соединяющем две другие точки расположенные внутри того же шара. Поэтому координаты рассматриваемой точки могут быть представлены как выпуклая линейная комбинация координат точек, расположенных на концах отрезка.

Множество точек внутри многоугольника образует выпуклое линейное пространство.

Приведем примеры точек, не образующих выпуклое линейное пространство.

Не образуют выпуклого множества точки на поверхности шара.

Не образуют выпуклого множества точки на периметре многоугольника.

Крайней (угловой) точкой выпуклого множества называют такую точку, которая не может быть представлена выпуклой линейной комбинацией двух других точек этого множества.