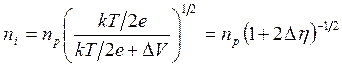
где
![]() — плотность ионов в переходной области
плазма — слой. Для максвелловских электронов плотность равна
— плотность ионов в переходной области
плазма — слой. Для максвелловских электронов плотность равна
![]()
При
![]() = 3— достаточно малой величине,
которую следует ожидать в области между границей плазмы и стенкой,
= 3— достаточно малой величине,
которую следует ожидать в области между границей плазмы и стенкой, ![]() 0,13. В этом случае обрезание электронного
распределения на стенке приведет к изменению плотности заряда вблизи стенки
приблизительно на 7% и к еще меньшему изменению в слое. Эффект будет малым. Для
значений
0,13. В этом случае обрезание электронного
распределения на стенке приведет к изменению плотности заряда вблизи стенки
приблизительно на 7% и к еще меньшему изменению в слое. Эффект будет малым. Для
значений ![]() 4
он быстро
становится пренебрежимо малым.
4
он быстро
становится пренебрежимо малым.
А. Приближенное описание слоя
Для
величин плотности плазмы, используемых для генерации ионных пучков с высокой
плотностью тока, плазменное решение, даваемое формулами (3.42) или (3.44),
пригодно вплоть до переходного слоя. Для указанных плотностей слой настолько
узок по сравнению с размерами плазменного объема, что доля генерируемого в
слое ионного тока пренебрежимо мала. Предположение, что все ионы образуются в
плазме, где изменение потенциала описывается плазменным решением, дает
возможность найти обобщенное решение в слое. Назовем это предположение
приближенным описанием слоя. Поскольку распределение ионов по скоростям на
границе плазмы, т. е. при ![]() , как было показано
выше, не зависит от природы ионизации, можно без потери общности упростить
анализ, предположив, что ионизация однородна в пространстве. В соответствии со
сделанным предположением, изменение потенциала в слое не зависит от функции
ионизации, т. е. от величиныγв выражении (3.37).
, как было показано
выше, не зависит от природы ионизации, можно без потери общности упростить
анализ, предположив, что ионизация однородна в пространстве. В соответствии со
сделанным предположением, изменение потенциала в слое не зависит от функции
ионизации, т. е. от величиныγв выражении (3.37).
Напишем
полное уравнение (3.36) системы плазма — слой при
g=const и![]() .
Получим
.
Получим
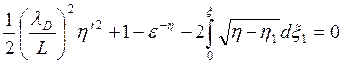 . (3.72)
. (3.72)
Используя
сделанное предположение, возьмем ![]() для слоя и
проинтегрируем только до
для слоя и
проинтегрируем только до ![]() . Заменим переменную интегрирования
. Заменим переменную интегрирования ![]() на
на ![]() с помощью плазменного решения (3.42)
с помощью плазменного решения (3.42)
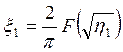
при постоянной скорости ионизации. Как было указано выше,
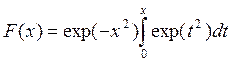 (2.129)
(2.129)
Дифференцируя
[или полагая ![]() = 0 в (3.63)], получим
= 0 в (3.63)], получим
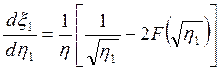 , и
можно переписать (3.27) в виде
, и
можно переписать (3.27) в виде
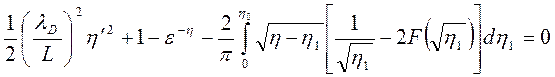 (3.73)
(3.73)
Заменим
пространственную переменную ![]() на
на ![]() , где a - расстояние до стенки. При этом, во-первых, пространственным
масштабом становится дебаевская длина (а не размеры плазмы), и, во-вторых,
расстояние отсчитывается внутрь слоя от стенки, а не от центра плазмы,
уравнении (3.73) преобразуется только производная
, где a - расстояние до стенки. При этом, во-первых, пространственным
масштабом становится дебаевская длина (а не размеры плазмы), и, во-вторых,
расстояние отсчитывается внутрь слоя от стенки, а не от центра плазмы,
уравнении (3.73) преобразуется только производная
![]() ,(3.74)
,(3.74)
так что (3.73) примет вид
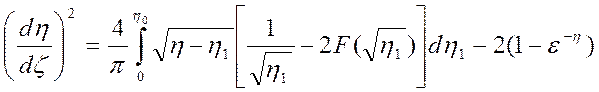 (3.75)
(3.75)
Первое слагаемое под интегралом легко вычисляется
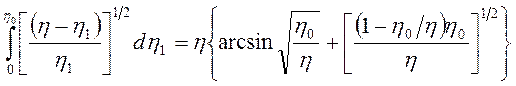 ,
(3.76)
,
(3.76)
тогда получим
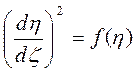 ,
(3.77)
,
(3.77)
где
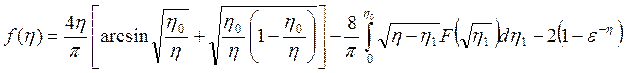 . (3.78)
. (3.78)
Поскольку
![]() уменьшается с ростом
уменьшается с ростом ![]() , из (3.77) следует
, из (3.77) следует
![]() , (3.79)
, (3.79)
так что
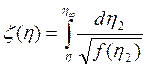 , (3.80)
, (3.80)
где
индекс «2» используется для того, чтобы отметить разницу между переменной
интегрирования и переменной ![]() , выступающей в
качестве нижнего предела. Величина
, выступающей в
качестве нижнего предела. Величина ![]() соответствует потенциалу
стенки. Для того чтобы полностью представить
соответствует потенциалу
стенки. Для того чтобы полностью представить ![]() ,
перепишем (3.78) ,
,
перепишем (3.78) ,
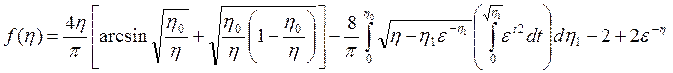 . (3.81)
. (3.81)
Найти
аналитическое решение не представляется возможным, но результаты численного
интегрирования при ![]() =20приведены в табл. 3.1
и показаны на рис. 3.12. При потенциале стенки
=20приведены в табл. 3.1
и показаны на рис. 3.12. При потенциале стенки ![]() <20
кривая на рис. 3.12 просто сдвигается вправо.
<20
кривая на рис. 3.12 просто сдвигается вправо.
Авторы
работы [43] рассмотрели слой, используя полное уравнение плазма — слой в форме
(3.35). Физическая природа сделанных ими предположений завуалирована
математической сложностью анализа; однако эти предположения, по-видимому,
идентичны сформулированным выше, а кривая на рис. 3.12 соответствует полученной
ими кривой ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.