Бесстолкновительная плазма. Дебаевская длина экранирования, страница 7

где ξ= r/L.Как и в плоском случае, решение в плазме получается при отбрасывании первого члена.

Решения в конечном виде типа (3.42) — (3.44) не найдены, но Тонкие и Ленгмюр [269] получили представления в виде рядов. Для рассматриваемой нами бесстолкновительной плазмы кривые похожи на зависимости для плоской геометрии, но в цилиндрической геометрии для потенциала поворота имеем при g~n_e

η =1,155    при   ξ₀ = 0,7722,                                                         (3.53)

а при g=const

η₀=1,26    при   ξ₀ = 0,638.                                                             (3.54)

Для сферической геометрии при g = const

ξ = 1,50при   ξ₀=0,818,                                                              (3.55)

а решение для случая g~n_eполучено с точностью, недостаточной для определения η₀ и ξ₀ .

Насколько известно автору, решения для g~n_e²в сферической или цилиндрической геометрии не опубликованы.

3.6. Распределение ионов по скоростям

Можно сразу рассчитать распределение ионов по скоростям, совместимое со сделанными вразд. 3.5 допущениями о том, что ионы возникают с нулевой скоростью и не сталкиваются.

Рассмотрим только плоский случай. Перепишем выражение (3.29) без интеграла

                                         (3.56)

для парциальной плотности в точке хионов, образующихся в интервале (х₁, x₁ + dx₁). Поскольку скорость определена формулой (3.30), можем перейти от дифференциала dx₁кскоростным переменным

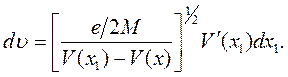(3.57)

Так как V'(x)отрицательна, то дифференциал dv(3.57) отрицателен при положительном приращении dx₁. Поскольку нас интересует разброс по скоростям ионов в интервале dx₁, запишем

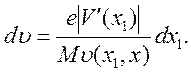(3.58)

Разрешим это выражение    относительно dx₁и  подставим результат в   (3.56), заменив также gсогласно   (3.37). Тогда получим

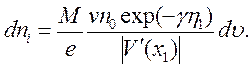                                                      (3.59)

В безразмерных переменных,    согласно    (3.31)    и   (3.34), имеем

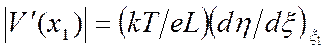, введя безразмерную скорость

,                                                                    (3.60)

найдем, что         

,                           (3.61)

где производная (dξ/dη)в точке η₁ заменила величину, обратную производной (dη/dξ) в точке ξ₁. Таким образом, нормированная функция распределения равна

            (3.62)

Производную (dξ/dη)можно определить на (3.42) — (3.44) при γ = 0, 1 или 2. В результате имеем

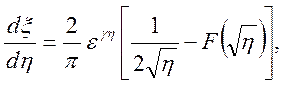                                                (3.63)

где -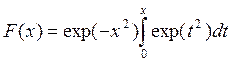 — определенный  выше   (2.129)

интеграл Доусона. В результате функция распределения

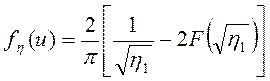                                                   (3.64)

оказывается одной и той же для γ = 0, 1, 2. Действительно, Чен [47] показал, что функция распределения вообще не зависит от механизма ионизации. Заметим, что в безразмерных переменных уравнение (3.30) имеет вид

                                                                   (3.65)

и (3.64) можно записать в более удобной форме

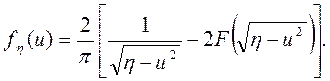                                                  (3.66)

Эта зависимость нанесена для различных значений η на рис. 3.10. Бесконечность при возникает потому, что (dη/dξ)=0 приη = 0. Это не приводит к неприятностям, поскольку сингулярность интегрируема. Разумеется, в действительности сингулярность должна исчезнуть, коль скоро мы учтем наличие начальных скоростей ионов или столкновения. Не следует ожидать, что такой учет приведет к существенным изменениям функции η(ξ).

3.7. Плотность ионного тока

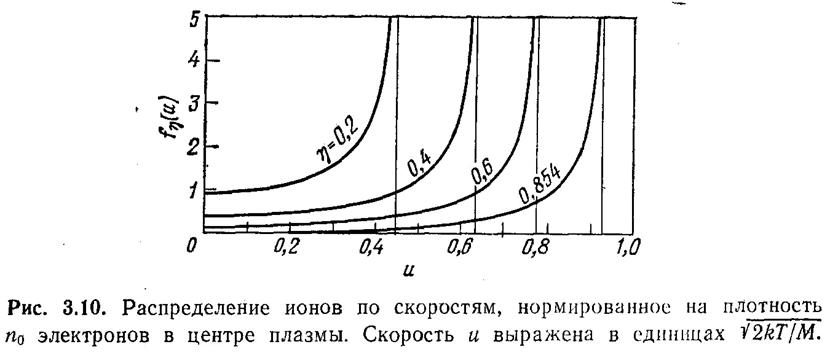
Число ионов в единичном интервале по скорости, если его разделить на n₀, т. е. на число ионов или электронов в центре плазмы, будет одним и тем же, как было показано выше, для любой скорости ионизации g(x). Тогда в плоской геометрии ионный ток из плазмы также будет одинаковым во всех случаях. Если это так, то можно рассмотреть только простейший случай постоянной скорости ионизации и получить общий результат. В нашем случае плотность тока на стенку задается выражением

J = ega,(3.67)

где g— постоянная скорость ионизации в единице объема, а— расстояние, с которого собираются ионы. Но из (3.47) следует