Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 3

Подстановка выражения (2) в уравнение (1) после интегрирования дает соотношение, выражающее теорему Буша:

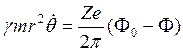                                                                                       (3)

где — значение  при  = 0. Уравнение (3) может быть формально записано как закон сохранения обобщенного момента импульса Р_θ в виде

                                                                                     (4)

где - азимутальная составляющая магнитного вектор-потенциала, единственного потенциала, существующего в осесимметричном пучке.

Уравнение параксиального луча выводится путем комбинирования характеристик параксиальных полей» закона сохранения обобщенного момента импульса и закона сохранения энергии. Мы начнем с приравнивания радиального ускорения силе Лоренца, действующей на ионный пучок, что дает

                                                        

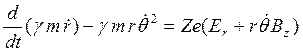
Использование теоремы Буша [уравнение (3)] и условия, что B_z не зависит от радиуса r, позволяет исключить в последнем выражении  и получить уравнение параксиального луча

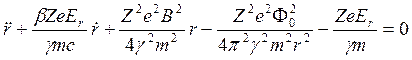                                             (5)

в котором время является независимой переменной, а для у использована приближенная формула  .  Однако более полезна такая форма уравнения (5), в которой независимой переменной является z. При условии, что , можно привести уравнение (5) к виду

                   (6)

где штрихи обозначают производные по z, а тот факт, что div Е = 0, позволил представить радиальное электрическое поле в релятивистском пределе формулой

                                                                            (7)

Более удобная форма уравнения (6) получается при использовании замены

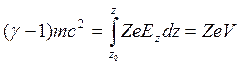
где V— потенциал, определяющий ускорение ионов при движении из точки z_o, в которой кинетическая энергия ионов равна нулю. Следовательно, если Vо определить выражением V₀ = mc²/Ze, то  и  что даёт

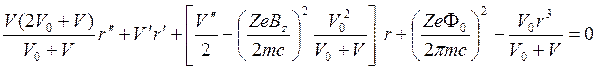             (8)

Если присутствуют только электрические поля и частицы являются нерелятивистскими (т. е. Vо » V), уравнение (8) приводится к более известному виду

                                                                                                   (8а)

4.1.2. Решения уравнения параксиального луча и матричный метод

Удобно преобразовать уравнение (8) путем замены зависимой переменной к более удобному виду. Лосон [2] использовал преобразование

                                                                                                           (9)

и, положив обобщенный момент импульса равным нулю, получил

 

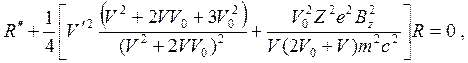
или                                                                                                                            (10)

Уравнение (10) имеет решение

                                                                                                                  (11)

где  и  - начальные значения и при z = z_o, а C(z) и S(z) - два независимых решения однородного уравнения

с начальными условиями

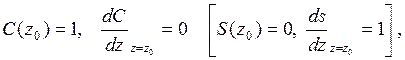
которые могут быть получены из уравнения (11) и его первой производной относительно z. Кривые С и S как функции z называются соответственно косинус- и синус-траекториями.

Следовательно, мы можем связать функции R(z) и R'(z) с их начальными значениями путем линейного преобразования вида

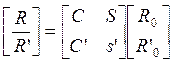                                                                                                                       (12)

Матрица такого преобразования имеет детерминант» равный единице, так как

                                                              (13)

Несколько простых примеров пригодности этого метода для описания траекторий ионов дается ниже. Пролетное пространство может быть представлено матрицей

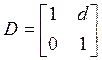
детерминант которой равен единице. Тонкие электростатические и магнитные линзы могут быть выражены формулой

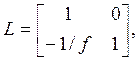
где положительно для собирающих линз и отрицательно для рассеивающих. Используя, как в световой оптике, понятие «главная плоскость», толстую линзу можно представить как комбинацию пролетных пространств и тонких линз.