Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 18

Чтобы точно измерить наклон траектории, практически всегда используется двухщелевой метод (рис. 4.18). Пространственное положение фронтальной щели определяет положение пучка, тогда как при помощи задней щели измеряют наклон и угловое распределение траекторий, проходящих через фронтальную щель. Многие методы основаны на указанной схеме [31]. Более современный вариант двухщелевого метода, позволяющий очень точно выполнять измерения эмиттанса, был изобретен Аллисоном [32]. В этом варианте электростатические отклоняющие пластины сохраняют фиксированное положение

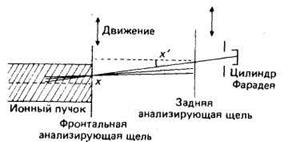
Рис. 4.19. Схема измерения эмиттанса, устраняющая необходимость двух независимых механических перемещений.

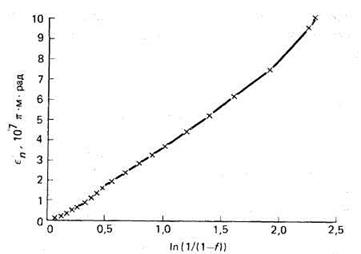
Рис. 4.20. Зависимость нормализованного эмиттанса еп внутри контура, содержащего долю f всех частиц пучка, от ln [1/(1 - f)]. Типичные данные для ионного пучка, вытянутого из многополюсного источника.

задней щели относительно фронтальной щели, таким образом сводя независимое движение обеих щелей к движению всей системы в целом (рис. 4.19).

Данные, полученные с помощью этих методов, могут быть проанализированы с помощью уравнения (93). На рис. 4.20 приведены результаты, полученные для слаботочного (8 мА) пучка ионов Н ^- [33]. Данные укладываются на прямую линию; это значит, что пучок может быть описан гауссовым или максвелловским распределением. Поперечная температура ионов в этом случае равна 0,25 эВ.

4.4.4. Эмиттанс и распространение пучка

Уравнение параксиального луча для одной из поперечных плоскостей в пучке может быть записано в форме

           (103)

где  и — сумма внешних фокусирующих сил и линейных самофокусирующих сил в пучке с однородной плотностью. Это уравнение часто называют уравнением Хилла. Его решение может быть выражено в виде

                                                                                                                         (104)

                                                                               (105)

Где . Подстановка решения в (103) показывает, что  должнo удовлетворять уравнению

                                                                                                                                  (106)

При исключении из (104) и (105) членов, содержащих , получается следующее выражение:

                                                                                                                    (107)

Где                                                                                                  (108)

Уравнение (107) описывает эллипс в плоскости , и точки с различными значениями 5 будут следовать по эллиптическим орбитам, так как они движутся вдоль оси z под действием сил, описываемых уравнением Хилла. Частицы, которые имеют различные значения а будут двигаться по аналогичным эллипсам, которые будут меньше или больше, но будут иметь ту же ориентацию относительно осей и . Площадь эллипса, описываемого уравнением (107), дается формулой

                                                                                                                     (109)

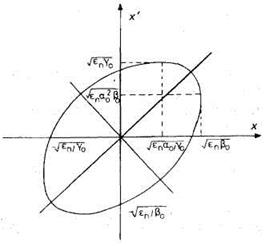
Рис. 4.21. Диаграмма эмиттанса пучка площадью πε_n и параметры Куранта—Снайдера α₀,β_0,γ₀, связанные с радиусом и углом расходимости пучка, как показано на рисунке.

Если пучок содержит ансамбль траекторий с различными значениями а, они представляют собой ряд вложенных эллипсов постоянной формы. Следовательно, плотность числа частиц является постоянной, как и следует из теоремы Лиувилля. Таким образом, площадь S идентична нормализованному эмиттансу, умноженному на π. Огибающая пучка, на которой X(z) достигает максимума для данной площади S, определяется соотношением

                                                                                                                                                (110)

а угол расходимости пучка  —

                                                                                                                                                    (111)

Уравнение эллипса, окружающего пучок (рис. 4.21), следовательно, есть