Угловой коэффициент касательной к графику функции равен производной этой функции, вычисленной в точке касания. Прежде всего, надо дать определение касательной к произвольной линии. Касательная к линии есть предельное положение МТ секущей MM1, когда точка M1, стремится по линии к точке М (рис. 2.6).
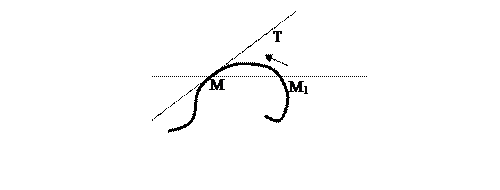
Рис. 2.6
Точка М называется точкой касания.

Рис. 2.7
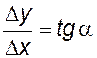 при
при ![]()
![]()
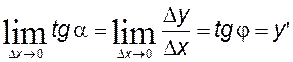
Итак, производная функции y=f(x) в данной точке есть тангенс угла наклона касательной к графику функции в этой точке.
Мы рассмотрели ряд задач из физики и геометрии, при решении которых появляется производная. Число подобных задач будет увеличиваться по мере изучения математики, физики и техники: всюду, где надо охарактеризовать скорость изменения функции, появляется производная. Отыскание производной называется дифференцированием.
Докажем ряд теорем о функциях, имеющих производные:
Теорема 1. Если функция имеет производную, то она непрерывна.
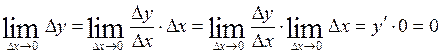 , что и требовалось доказать.
, что и требовалось доказать.
Обратное утверждение неверно. Функция y=|x|непрерывна при х = 0, но производной в этой точке не имеет.
Теорема 2. (правила вычисления производных) Если функции: и = и(х) и v = v(x) имеют производные, то
I.
![]()
II.
![]()
III. (Си)' = Си' (С—постоянная);
IV.
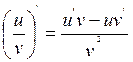
Доказательство:
По определению производной, имеем
I.
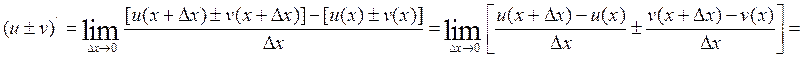
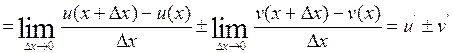
II.
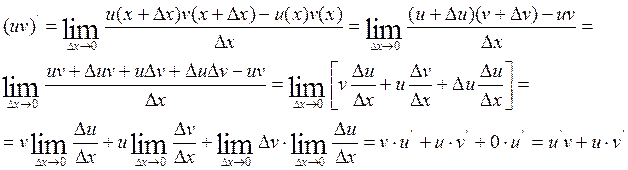
III.
![]() так
как
так
как ![]()
IV.
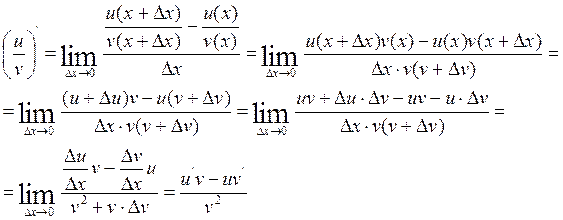
Следующие теоремы рассмотрим без доказательств.
Теорема 3. (производная сложной функции). Пусть функции y = f(t) и t = g(x) имеют производные. Тогда сложная функция y= f(g(x)) имеет производную и
![]()
Теорема 4. (производные обратных
функций). Производные от взаимно обратных функций обратны по величине. Записывают
это так 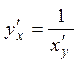 или
или 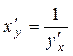 .
.
Например, ![]() ,
, ![]() ,
, ![]() . Следовательно
. Следовательно 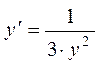 .
.
Теорема 5. Дифференцирование функций заданных неявно
f(x,y)=0 неявный вид функции
При задании функции в неявном виде, находят производные левой и правой части уравнения, а затем выражают y'
Пример: x2+y2=R2, R=const, 2x+2y y'=0, y'=-2x/(2y)=- x/y
Метод логарифмического дифференцирования
В случае если функция задана в виде y=uv то она называется показательно - степенной. Чтобы найти производную данной функции необходимо перед дифференцированием провести логарифмирование.
![]()
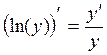 ,
, 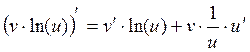
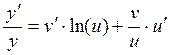
![]()
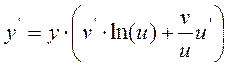 т.к. y=uv
т.к. y=uv
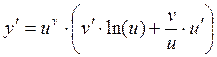
Пример: y=xx
![]() ,
, 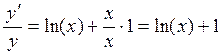 ,
,
![]() .
.
Этот метод также
используют для дифференцирования сложных выражений, в которых есть
произведения, частное, всевозможные степени. Пример: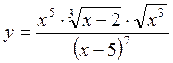 ,
,
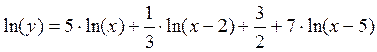
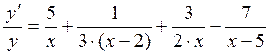
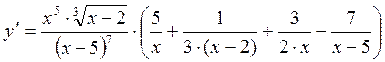
Производные основных элементарных функций составляют таблицу основных производных:
I. ![]() VIII.
VIII. ![]()
II. ![]() IX.
IX. 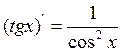
III. ![]() X.
X. 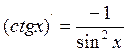
IV. ![]() XI.
XI. 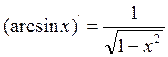
V. ![]() XII.
XII. 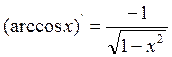
VI. 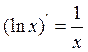 XIII.
XIII. 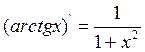
VII. ![]() XIV.
XIV. 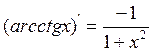
Производная ![]() в
свою очередь есть функция от х. Может оказаться, что эта
функция имеет производную; эта производная называется второй производной
от функции у = f(х) и
обозначается f" (х) или у",
так что
в
свою очередь есть функция от х. Может оказаться, что эта
функция имеет производную; эта производная называется второй производной
от функции у = f(х) и
обозначается f" (х) или у",
так что ![]() или
или ![]() .
.
Все производные, начиная со второй,
называются старшими производными, или
производными высших порядков. Производная ![]() называется
первой производной.
называется
первой производной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.