Производная функции. Пример задачи приводящей к понятию производной. Физический смысл производной, страница 2

Теорема 1. Если функции f(х) и g(x) непрерывны в точке х₀, то функции f(х) ±g(х) непрерывны в точке х₀.

Возьмем число ε > 0. Число ε/2 > 0, и в силу непрерывности функции f(х) в точке х₀ можно подобрать такое число δ₁ > 0, что

|f(x)−f(x₀)|< ε/2 для всех х, для которых |х−х₀| < δ₁ , а в силу непрерывности функции g(x) в точке х₀ для числа ε/2 > 0 можно подобрать такое число δ₂ > 0, что

|g(x)−g(x₀)|< ε/2 для всех x, для которых |х−x₀| < δ₀. Возьмем δ =min(δ₁; δ₂); тогда для любого х, удовлетворяющего   неравенству |х−х₀|< δ, будут выполнены оба первых неравенства, и потому

|[f(x)+g(x)]-[f(x₀)+g(x₀)]|≤|f(x)-f(x₀)|+|g(x)-g(x₀)|< ε/2+ ε/2= ε

Так как эти вычисления верны при любом ε > 0, то непрерывность функции f(x) + g(x) в точке х₀ доказана. Непрерывность функции f(x)−g(x) доказывается аналогично.

Теорема 2. Если функция t=g(х) непрерывна в точке х₀, а функция y = f(t) непрерывна в точке t₀ = g(x₀), то сложная функция f(g(x)) непрерывна в точке х₀.

Возьмем число ε > 0. Так как функция f(t) непрерывна в точке t₀ = g(x₀), то можно подобрать такое число δ₁ > 0, что

|f(t)−f(t₀)|< ε для всех t, для которых |t−t₀|< δ₁

А  так   как   функция   t = g(x) непрерывна в точке х₀, то для   положительного   числа   δ₁   можно   подобрать   такое число δ > 0, что |g(x) −g(x₀)|< δ₁ для всех х, для которых |х − х₀| < δ.

Возьмем любое число х такое, что | х − х₀| < δ. Что можно сказать о |f(g(x)) − f(g(x₀))| ? Посмотрим, как получены числа y = f(g(x)) и y₀ = f(g(x₀)). Сначала находятся (в силу определения) числа t = g(x) и t₀ = g(x₀), имеем |t−t₀|=|g(x)−g(x₀)|< δ₁. По этим числам находятся у = f(t) и y₀ = f(t₀), для которых |у−y₀|=|f(t)−f(t₀)|< ε. Таким образом, |f(g(x)) – f(g(x₀))|< ε.

Так как все эти вычисления проведены для любого ε > 0, то непрерывность функции f(g (х)) в точке х₀ доказана.

Теорема 3. Если функции f(х) и g(x) непрерывны в точке х₀, то функции k·g(x) (k - постоянная), f(x)·g(x) и  f(x)/g(x) (последняя при условии g(x₀)≠0) непрерывны в точке х₀.

Так как линейная функция l(t)=ktнепрерывна всюду, то в силу теоремы 2 сложная функция l(g(х)) = kg (x) непрерывна в точке х₀.Остальные утверждения оставим без доказательств, считая их верными.

Теорема 4.Если функция f(х) непрерывна в точке х₀ и f(х₀)>0, то можно указать такое δ > 0, что f (х) > 0 для любых х таких, что |х - x₀|< δ.

Возьмем ε=f(x₀) > 0 и по нему найдем δ > 0 (в силу непрерывности f (х) такое, что

| f(х) -f(х₀)| <f (х₀) для любых х таких, что|х - x₀|< δ.

Тогда для всех таких х будет f (х) - f(x₀)> - f(x₀),   или f(х) > 0, что и требовалось доказать.

Геометрически теорема 4 сразу видна на рис. 2.4. Аналогичное заключение верно и при f(x₀) < 0.

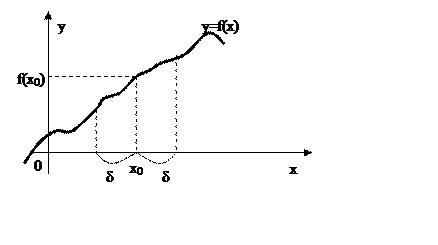
Рис. 2.4

2.2. Пример задачи приводящей к понятию производной.

Различные задачи естествознания − такие, как определение скорости, ускорения, силы тока, плотности вещества и многие другие - приводят к одним и тем же математическим вычислениям. Их решение приводит к понятию производной. В этом можно убедиться, рассмотрев некоторые простые явления. Например: скорость  прямолинейного  движения. Пусть тело движется прямолинейно по известному закону S = f(t). Если движение было равномерным и за время ∆tтело прошло путь ∆S, то скорость vбудет равна отношению приращения пути ∆S к приращению времени ∆t: 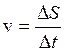. Для переменного движения отношение 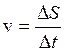 определяет величину средней скорости: 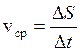. Но знание средней скорости не дает полной картины движения, так как различным видам движения может соответствовать одна и та же скорость v_ср. На рис. 2.5 приведены различные графики  пути в интервале времени ∆t: АСВ, AC₁ B, АС₂ В, для которых средняя скорость одна и та же.