Производная функции. Пример задачи приводящей к понятию производной. Физический смысл производной

§2.  Производная функции  

2.1. Непрерывность функции.

В математическом анализе в основном рассматриваются непрерывные функции.  Ряд явлений в окружающем нас мире описывается непрерывными функциями. Слух, зрение, восприятие УЗ связаны с колебательными процессами, которые описываются непрерывными функциями.  Наблюдая происходящие вокруг изменения, прежде всего можно отметить, что они происходят (в основном) постепенно, непрерывно. Например, температура тела изменяется постепенно, без скачков, непрерывно, т. е. за малый промежуток времени температура изменяется мало. В этом примере, с точки зрения математика, температура тела есть функция времени, и эта функция такова, что при малом изменении аргумента (времени) мало меняется функция (температура).

Но что значит мало? Вот 1 мм — это много или мало? Если ошибка в 1 мм сделана при изготовлении протеза ноги, то это мало. Но если эта же ошибка в 1 мм сделана при изготовлении клапана сердца диаметром в 0,5 см, то это очень много. Таким образом, ответ на вопрос о том, будет ли взятая величина малой, зависит от обстоятельств. Эти соображения должны быть учтены при определении непрерывности функции.

Непрерывной функцией описывается количество поглощаемого кислорода в зависимости от массы животного.  Представление о непрерывности функции связано с тем, что ее графиком является плавная, нигде не прерывающаяся линия.

Рис. 2.1

y=f(x),    Δy=f(x₀+Δx)-f(x₀) – приращение функции если  Δx → 0,  то  Δy→ 0. Функция y=f(x) называется непрерывной в точке x₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Свойство непрерывности функции может выполняться в одних точках и нарушаться в других. Если некоторая функция в точке х₀ не является непрерывной, то эта точка называется точкой разрыва, а функция - разрывнойв данной точке. При этом предполагается, что функция f(x) определена в некоторой окрестности точки х₀; в самой же точке х₀ функция может быть как определена, так и не определена.

Зависимость величины возбуждения (например, нервных клеток, мышц и т. п.) от времени при внешних воздействиях изображается функцией, имеющей разрывы.

Если величину возбуждения Е измерить в тех или иных единицах, то график возбуждения E(t) имеет вид, показанный на рис. 2.2. В момент t = t₀ клетка получает сигнал. Возбуждение клетки происходит в момент t₁ > t₀. Отрезок [t₀, t₁] называется  периодом рефрактерности. В момент t₁, клетка мгновенно возбуждается до максимальной величины, а затем возбуждение постепенно уменьшается до тех пор, пока не будет дан новый сигнал. Если сигнала нет достаточно долго, то возбуждение становится равным нулю. На концах периодов рефрактерности функция E(t) имеет разрыв.

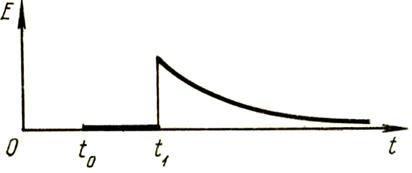
Рис. 2.2

Произвольный случай разрыва функции  в точке х₀.

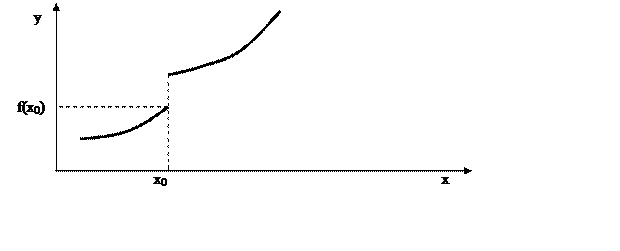
Рис. 2.3

Определение. Функция, f(х) называется непрерывной в точке х₀ если для любого положительного числа ε (ε > 0) можно подобрать такое положительное число δ (δ>0), зависящее от ε, что |f(х)-f(х₀)| < ε,  для всех x, которые удовлетворяют неравенству |x-х₀| < δ.             (1)

Подчеркнем, что по самому смыслу данного определения функция f(х) должна быть определена в некотором интервале, содержащем точку х₀.

Примеры. 1. Покажем, что линейная функция y=f(x)=3x+2 непрерывна всюду, т. е. в любой точке х₀.

Для того чтобы это доказать, надо проверить, что эта функция удовлетворяет определению. Для этого возьмем точку (число) х₀ и положительное число ε (ε>0) и постараемся подобрать δ>0 такое, чтобы выполнялось условие (1). Если рассматривать х только такие, что |x-х₀| < δ, то |f(x)-f(x₀)|=|3х+2-(3х₀ +2)| = 3|х-х₀|<3δ.                    

Отсюда   видно,  что достаточно взять δ = ε/3, чтобы было

|f(х)-f(х₀)| < ε.

Таким образом, для взятого ε > 0 нам удалось подобрать δ (δ=ε/3) такое, что выполнено условие (1).

Поскольку все проведенные выше вычисления проделаны для произвольного ε > 0, то этим доказана непрерывность функции у = 3x + 2 во взятой точке x₀. Точка х₀ тоже произвольна – при вычислениях никаких ограничений на х₀ не накладывалось. Следовательно, функция у = Зх+2 непрерывна всюду.

2. Рассмотрим общий случай линейной функции: y= f(x)= kx + b – и покажем, что она непрерывна всюду. Возьмем точку х₀, число ε > 0 и будем подбирать δ. Поскольку

|f(х)-f(х₀)| =|(kx+b)-(kx₀ + b)| =|k||x-x₀|<|k| δ  для всех х, удовлетворяющих неравенству |х-x₀|< δ, то из уравнения видно, что при k≠0 достаточно взять δ = ε/|k|, чтобы было  |f(х)-f(х₀) | < ε.

Таким образом, для взятого  ε > 0 мы подобрали δ = ε/|k| такое, что выполнено условие (1). Так как все приведенные выше вычисления проделаны при произвольном ε > 0, то этим доказана непрерывность функции y = kx+b (при k≠0) во взятой точке х₀. Но на точку х₀ тоже никаких ограничений при вычислениях не накладывалось, и, следовательно, функция y = kx+b (k≠0) непрерывна всюду. Если же k = 0, то y = f(x) = b (т. е. y – постоянная) и |f(х)-f(х₀)|=|b-b|=0 < ε  для любых х. Поэтому можно, например, взять δ=1.

Рассмотрим некоторые свойства непрерывных функций. Эти свойства формулируются ниже в виде теорем.