Высказывания. Операции дизъюнкции, конъюнкции и отрицания. Пропозициональные формулы, булевы функции и их количество. Класс монотонных функций. Полнота систем булевых функций, страница 8

Сочетание из n по kможно реализовать одновременной выборкой к шаров из имеющихся в урне n различных шаров.

§ 7. Беспорядки, латинские прямоугольники

Определение 1. Беспорядком называется такая перестановка чисел 1,2,... , n, в которой ни одно число i не находится на i-том месте.

Пример 1. Среди перестановок чисел 1,2,3 имеется два беспорядка: 312 и 2 31.

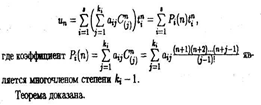
§ 5. Сочетания с повторениями

Определение 2. Латинским прямоугольником называется матрица m х n, составленная из чисел 1,2,... , n так, что ни в одной строке, ни в одном столбце этой матрицы числа не повторяются.

Если т равен своему максимально возможному значению п, то говорят о латинском квадрате. Имеется теорема, что любой латинский прямоугольник можно дополнить до латинского квадрата.

еcли в первой строке латинского прямоугольника m x n числа 1,2,... , n расположены в порядке возрастания, то остальные строчки являются беспорядками, поэтому количество латинских прямоугольников 2 х n равно 6_п.

ГЛАВА 4. ГРАФЫ

§ 1. Понятие графа. Матрица смежности и ее свойства

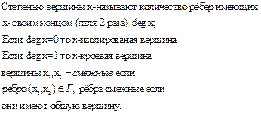
§ 6. Формула включений и исключений

§ 8. Производящие функции

§ 9. Линейные однородные рекуррентности

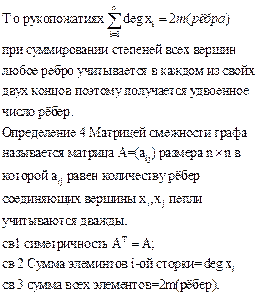
§ 2. Подграф. Частичный нулевой полный дополнительный графы, соединение графов.

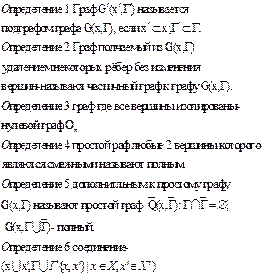
§ 3. Изоморфизм графов. Реализация графов в R₃

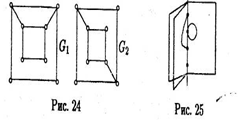
Определение 2. Говорят, что граф Gдопускает реализацию в пространстве R_n, если его вершинам можно сопоставить точки из R_n, , а ребрам сопоставить непрерывные кривые, соединяющие соответствующие точки так, чтобы эти кривые не имели внутренних точек пересечения с другими кривыми. Реализацией графа в R_n называется изображение, полученное при этом сопоставлении.

.

§ 5. Цепи, циклы, связность

Определение 1. Цепью (маршрутом) в графе G(X, Г) называется последовательность его ребер (v₀,v₁), (v₁,v₂), .. , (v_l-1,v_l); вершины v₀, v₁ являются концами цепи, длиной цепи называется число l, равное количеству ребер в этой цепи.

§ 7. Следствия из теоремы Эйлера о плоских графах

Теорема 1. Любой граф можно реализовать в трехмерном пространстве R.₃.

Доказательство. Пусть дан граф G(X, Г), X= {х₁, x₂,.. ,х_п}, а Г = (g₁,g₂, • • • ,g_т)- Возьмем в пространстве прямую Iи выберем на ней точки х'₁, х'₂,... , х_n', которые соответствуют вершинам x₁,x₂,.. ,х_п (см. рис. 25).

Через прямую l проведем т различных полуплоскостей и обозначим их П₁,П₂,..,П _m. Если ребро g_k = (Xi,Xj), где i <> j, то ему сопоставим полуокружность, которая лежит в полуплоскости П_к и опирается на точки x'_tи x'_j. Если ребро g_k = (х_i,-,x_i;,) является петлей, то ему сопоставим окружность, которая лежит в полуплоскости П_к . и касается прямой l в точке x'_i. Так проделаем для всех к = 1,2,... , т и в результате получим реализацию графа Gв трехмерном пространстве. Теорема доказана

.

§ 4. Плоские и планарные графы

Определение 1. Граф, допускающий реализацию на плоскости, называется планарным, а его реализацию на плоскости называют плоским графом.

§ 8. Эйлеровы графы. Задача о кенигсбергских мостах

Цепь называется простой, если все ее ребра различны.

Определение 1. Связный граф Gназывается эйлеровым, если существует простая замкнутая цепь, содержащая все ребра графа Gтакая цепь называется эйлеровой.

Теорема об эйлеровом графе. Связный граф является эйлеровым тогда и только тогда, когда все его вершины имеют четную степень.

Доказательство. Если граф G- эйлеров, то при каждом прохождении эйлеровой цепи через данную вершину х участвуют два ребра, поэтому deg х — четное число.

Наоборот, пусть Gимеет только четные вершины. Индукцией по числу ребер т докажем, что граф имеет эйлерову цепь.