

§ 2. Операции импликации, эквиваленции и суммы по модулю 2
Определение 1. Импликацией высказываний a и b называется высказывание "если а, то b" или "из a следует b", которое ложно лишь когда а истинно, но b ложно; обозначается импликация так: а à b, высказывание а называется посылкой, b — заключением. Значения импликации приведены в табл. 4.
Свойство 1. a à b =¬a V b — правило исключения импликации. Доказательство дано в табл. 4.
Определение 2. Эквиваленцией высказываний а и b, обозначается через а ~ b, называется высказывание "а эквивалентно b", которое истинно только, когда a = b, что и отражено в табл. 5.
Свойство 2. а ~ b = a* b V ¬a*¬b — правило исключения эквиваленции. Доказательство дано в табл. 5.
Свойство 3. а ~ b = (а àb)(b à а).
Доказательство. Преобразуем правую часть равенства:
(а à b)(b à а) = ![]()
Определение 3. Суммой по модулю 2 высказываний а и b,
обозначается a![]() b,
называется высказывание "или a, или bя, которое истинно, когда ровно одно из этих
высказываний является истинным (см. табл. 5).
b,
называется высказывание "или a, или bя, которое истинно, когда ровно одно из этих
высказываний является истинным (см. табл. 5).


§ 6. Теорема о сокращенной ДНФ. Минимизация
ДНФ
Свойство 1. При удалении любого сомножителя из элементарной конъюнкции ее область истинности расширяется в два раза.
Доказательство. Если элементарная конъюнкция К' получается из конъюнкции К удалением сомножителя xiqi, то К истинна только при одном значении Xi = qi, а К' истинна при двух значениях Xi = 0 и xi = 1. Свойство доказано.
Определение 1. Конъюнктом (импликантой) булевой функции f называется элементарная конъюнкция К, область истинности которой является подмножеством области истинности f.
Таким образом конъюнкт функции f является истинным на некоторых из тех строчек таблицы истинности, где истинна f, и является ложным на всех строчках, где ложна функция f.
Возьмем некоторый конъюнкт K0 функции f и удалим из него такой сомножитель, чтобы получилась элементарная конъюнкция К1, остающаяся конъюнктом этой функции. Таким же образом из К1 получим конъюнкт К2 и т.д. Поскольку при каждом удалении сомножителя область истинности конъюнкции расширяется в два раза, то на некотором этапе получится конъюнкт К, такой, что удаление любого его сомножителя приведет к элементарной конъюнкции, не являющейся конъюнктом функции f.
§ 8. Функциональные схемы
Определение 1. Функциональным элементом называется устройство, имеющее n упорядоченных входов и один выход; если на каждый из входов подать один из сигналов 0 или 1, то через время т на выходе будет результат: 0 или 1.
В дальнейшем будем рассматривать только случай T = 0, такие элементы называются 0-тактными.
Из определения следует, что каждый функциональный элемент реализует некоторую булеву функцию у — f(X1,X2,... ,хп), изображение см. на рис. 4.
Определение 2. Понятие функциональной схемы дается индуктивно:
1) любой функциональный элемент считается функциональной схемой, входами и выходом схемы являются входы и выход этого элемента;
2} если S0 и S1— функциональные схемы, то можно получить новую схему S, соединив выход S1 с одним из входов S0; при этом выходом S является выход So, а входами S будут все входы So и S1, кроме того входа So , с которым соединен выход S1 (см. рис. 5);
3) если S функциональная схема, то можно получить новую схему S1, отождествив (соединив) несколько входов 5; при этом выход S'' совпадает с выходом S, а входами S' являются входы S, при этом соединенные входы считаются за один вход (см. рис. 6). Из определения 2 следует, что любая функциональная схема реализует на выходе значение некоторой булевой функции от значений ее входов, эта функция получается суперпозициями из булевых функций, реализуемых функциональными элементами этой схемы и функций проецирования.
§ 12. Класс монотонных функций
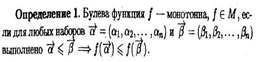
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.