Высказывания. Операции дизъюнкции, конъюнкции и отрицания. Пропозициональные формулы, булевы функции и их количество. Класс монотонных функций. Полнота систем булевых функций

§ 1. Высказывания. Операции дизъюнкции, конъюнкции и отрицания

Высказыванием считается повествовательное предложение, являющееся либо истинным, либо ложным. Мы не станем рассматривать высказывания с точки зрения их содержания и фактически будем отождествлять высказывание с его истинностностным значением. Произвольные высказывания будем обозначать буквами а, b, с, ... . Значение "истина" обозначается через 1 или true, a значение "ложь" - через 0 или false.

Определение 1. Высказывания а и 6 называются равносильными, обозначается, а = b, если они оба истинны, либо оба ложны.

Свойство 1. а =а.

Свойство 2. Если a=b, то b = a.

Свойство 3. Если a =b и b = с, то, а = с.

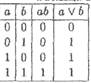Определение 2. Конъюнкцией высказываний а и b называется высказывание "а и b", которое является истинным лишь, когда каждое из высказываний а, 6 является истинным. Обозначается конъюнкция так: a*b, а /\ b, a&b,

a and b.

Свойство 4. а • 0 = 0.

Свойство 5. а • 1 = а.

Свойство 6. a • а = а —идемпотентность.

Свойство 7. a•b = b•а — коммутативность.

Свойство 8. а(bс) = (аb)с — ассоциативность.

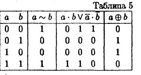
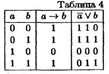
Свойство 4.

Доказательство этого свойства непосредственно следует из определения эквиваленции и суммы по модулю 2 (см. табл. 5).

Свойство 5

Свойство 6 

Свойство 7 

Свойство 8 

Свойство 9  

Свойство 10 

Определение 3. Дизъюнкцией высказываний о и b называется высказывание "а или b^я, которое истинно, если хотя бы одно из высказываний а, b является истинным, что и отражено в табл. 1. Обозначается значение дизъюнкции так : а V b,

a or b

Свойство 9. а V 0 = а.

Свойство 10. а V 1 = 1.

Свойство 11. a V a = a — идемпотентность.

Свойство 12. а V b = b V а — коммутативность.

Свойство 13. a V (b V с) = (a V b) V с — ассоциативность. 

Доказательство. Сделаем разбор случаев по переменной 6; для этого найдем значения левой части (LP) и правой части (АР) для b = 0 и для b=1.

Пусть b = 0, тогда LP = a V (0 V c) = a V c,

RP=(a V 0) V c = — aVс; отсюда следует, что LP = RP.

Пусть b = 1, тогда LP = a V(l V c) = a V l =1,

RP= (a V l) V c = = l V c = l; отсюда следует, что LP = RP.

Итак, в каждом из двух возможных случаев, значения левой и правой частей свойства 13 совпадают, что и требовалось доказать.

Свойство 14. а (b V с) = ab V ас.

Свойство 15. a V bc = (a V b)(a V с).

Докажем свойство 15.

В табл. 2 для всех возможных значений а, b, с приводятся результаты выполнения операций V и /\ в левой и правой частях данной формулы. Столбцы, выделенные жирным шрифтом, являются итоговыми значениями левой и правой частей и поскольку эти столбцы одинаковы, то свойство 15 доказано.

§ 3. Пропозициональные формулы, булевы функции и их количество

Определение 1. Пропозициональной формулой (ПФ) называется формула, составленная из логических констант 0 и 1, логических переменных, принимающих эти значения 0 и 1, с помощью скобок и знаков логических операций.

Для уменьшения количества скобок устанавливают следующие приоритеты для логических связок:

Для пропозициональной формулы A(x₁,x₂,...,х_п) можно составить истинностную таблицу ее значений для всех наборов значений логических переменных x₁,x₂,...,х_п Эта таблица имеет 2ⁿ строчек. Значения переменных x₁,x₂,...,х_п записывают переводя числа 0,1,2,... , 2ⁿ — 1 в двоичную систему счисления в порядке их возрастания (см. табл. 1 ,5).

Определение 2. Функция у = f(x₁,x₂,...,х_п) называется булевой (БФ), если x_i € {0; 1} при i = 1,2,... ,n, у € {0; 1}.

Булевы функции можно задавать истинностными таблицами, а также указывать правило их вычисления с помощью пропозициональных формул.

Определение 1. Дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ). Дизъюнкция полных элементарных конъюнкций называется совершенной ДНФ.

Теорема о реализации булевой функции в ДНФ. Для любой булевой функции f(x₁,x₂,.. , х_п) имеет место формула

Доказательство. При фиксированных значениях x₁,x₂,.. , х_п конъюнкция x^q1₁,x^q2₂,.. , х^qn_п истинна лишь тогда, когда q_i = x_i для всех значений i = 1,2,... , п. Следовательно, в правой части формулы (1) может быть отличной от 0 только одна элементарная конъюнкция f(x₁,x₂,.. , х_п,x₂,.. , х_п)x^x1₁,x^x2₂,.. , х^xn_п равная  f(x₁,x₂,.. , х_п,x₂,.. , х_п). Теорема доказана.

Теорема о количестве булевых функций.

Имеется различных булевых функций от n переменных.

Доказательство. Если функция имеет n переменных, то в ее истинностной таблице имеется 2ⁿ строчек. Поскольку в каждой строчке булева функция может принимать два значения 0 и 1, то всего имеется  различных булевых функций от n переменных. В табл. 6 приведены все 16 булевых функций от двух переменных а и b.

Если булева функция от n переменных задана стандартной таблицей, строчки которой являются двоичными числами, расположенными в порядке возрастания от 0 до 2ⁿ — 1, то достаточно указать столбец значений функции. Этот столбец можно написать целиком, однако часто указывают только номера строчек, на которых функция истинна.

Определение 3. Переменная Х_i называется существенной для функции у = f(x₁,x₂,--- ,x_n), если можно указать такие значения