Excel, решение численных задач, линейных и нелинейных уравнений, страница 10

Здесь искомая функция изображена линией с ординатами Y0, Y1, Y2, ..., Yk+1 (пустые прямоугольники), а полученная по методу Эйлера – ломаной с ординатами Y^0, Y^1, Y^2, ... , Y^k+1 (черные прямоугольники). Если DХ мало – можно полагать, что уравнение касательной к искомой функции в точке Х0 (прямая Y0Y^1) не сильно отличается от Y(Х) на участке DХ (дуга Y0Y1). Найдем Y1

Y^1 = Y0 + DY1 = Y0 + DХŸTg(W0).

Тангенс W0 равен значению производной функции Y(Х) в точке Х0, которую легко вычислить

TgW0 = Y'0 = Z(X0,Y0).

И можем записать  Y^=Y0 + DХŸZ(X0,Y0).

Следующий шаг – проведение касательной к Y(Х1), т.е. построение участка с тангенсом наклона, равным Z(X1,Y1). Однако поскольку нам известно не точное значение Y1, а приближенное Y^1, проведем линию с тангенсом угла наклона, равным Z(X1,Y^1).

Тогда       Y^2 = Y^1 + DХŸZ(Х^1,Y^1).

Отсюда можем получить рабочие формулы метода

Хk+1 = Хk + DХ     

и  Yk+1 = Yk + DХŸZ(Хk,Yk).

Метод является весьма приблизительным (сравните вычисленную и настоящую функции на рисунке). Уменьшив шаг интегрирования DХ, можно добиться приемлемой погрешности. При DХÞ0 решение сходится к точному.

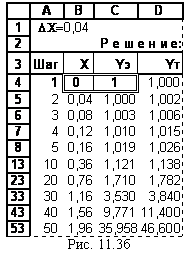
На рис. 11.3б и 3в представлены (в числовом и формульном виде) таблицы решения дифференциального уравнения вида

2xy      = 0 

при начальных условиях Y(0)=1.

Решение Y=exp(X2) такого простого урав­нения известно, что позволит нам оценить точность вычислений в таблице. Здесь в ячейке В1 установлен шаг интегрирования 0,4, в В4 и С4 – начальные условия уравнения. Текущие значения номера шага и значения Х вычисляются аналогично предыдущему. В колонке Yэ находится решение по методу Эйлера, а в колонке Yт – предъявляется точное решение с непосредственным использованием функции exp(X2). Решение доведено до Х=1,96 (50 шагов).