Собственные векторы и собственные числа линейного преобразования. Билинейные и квадратичные формы, страница 9

(Форма является невырожденной и все  либо , либо  ).

Доказательство. Так как случаи положительно и отрицательно определённой формы рассматриваются аналогично, то доказательство проведём для положительно определённых форм.

1)  Пусть  - положительно определённая квадратичная форма, тогда формула (7.12) принимает вид

(иначе  такой, что   и ).

Если при этом , то отсюда следует, что для ненулевого вектора  с координатами ,  значение формы  обращается в 0, а это противоречит определению положительно определённой квадратичной формы, следовательно .

2)  Пусть , тогда (7.12) имеет вид

.

Ясно, что : ,  причём, если , то

,   т.е. , следовательно, форма положительно определённая.

Теорема 7.8. (Необходимое и достаточное условие неопределённости квадратичной формы).

Квадратичная форма  является знакопеременной тогда и только тогда, когда .

Доказательство.

1)  Так как знакопеременная форма принимает как положительные, так и отрицательные значения, то её представление (7.12) в нормальном виде должно содержать как положительные, так и отрицательные слагаемые (в противном случае эта форма принимала бы либо неотрицательные, либо неположительные значения). Следовательно, как положительный, так и отрицательный индексы инерции отличны от 0.

2)  Пусть , . Тогда для вектора  с координатами ,  имеем , а для вектора  с координатами ,  имеем , следовательно форма знакопеременная (см. определение). 

Теорема 7.9. (Необходимое и достаточное условие полуопределённости квадратичных форм).

Квадратичная форма  является полуопределённой тогда и только тогда, когда либо , , либо , .

Доказательство.

1)  Пусть  - положительно полуопределённая квадратичная форма. Тогда, очевидно,  и  (иначе, если  форма является положительно определённой).

2)  Если , , то  и  с координатами ,  такой, что , следовательно,  - положительно полуопределённая квадратичная форма.

Замечание. При применении этих признаков квадратичную форму необходимо привести к каноническому виду, что не всегда удобно и достаточно долго.

Поэтому необходимо иметь критерий, с помощью которого можно классифицировать форму, не приводя её к каноническому виду.

Теорема 7.10. (Критерий Сильвестра).

Квадратичная форма  является положительно определённой тогда и только тогда, когда .

Квадратичная форма  является отрицательно определённой тогда и только тогда, когда  т.е.   ().

Доказательство.

1)  Докажем сначала, что из условия знакоопределённости квадратичных форм следует, что  ().

Доказательство проведем от противного.

Пусть, например,  (). Рассмотрим следующую однородную систему линейных уравнений

  .

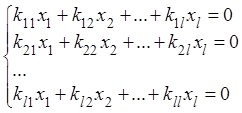Так как  – определитель этой системы и , то система имеет нетривиальное решение  (). Умножим первое уравнение на , второе на ,  …,  последнее на  и сложим полученные равенства. В результате получим равенство 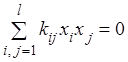, левая часть которого представляет собой значение квадратичной формы  на ненулевом векторе  с координатами  и это значение равно 0, что противоречит знакоопределённости формы.

Итак, мы убедились, что  (). Поэтому можно применить метод Якоби приведения формы  к каноническому виду и воспользоваться формулами (7.6) для канонических коэффициентов 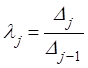. Если   – положительно определённая, то из теоремы 7.7 следует, что , следовательно,

, так как , , ,  …,

.

Если   – отрицательно определённая квадратичная форма, то все канонические коэффициенты отрицательны (теорема 7.7), следовательно, ,  ,  ,  …, и знаки главных угловых миноров чередуются .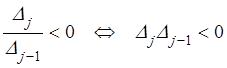

2)  Достаточность. Пусть выполнены условия, наложенные на главные угловые миноры  в формулировке теоремы. Так как  (), то форму  можно привести к каноническому виду методом Якоби, причём по формулам (7.9) 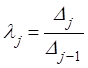 и если :  , то и :  , т.е. форма положительно определенная (теорема 7.7).

Если же знаки  чередуются и , то из соотношений (7.6) следует, что  и форма отрицательно определёна (теорема 7.7). Теорема доказана полностью.