Собственные векторы и собственные числа линейного преобразования. Билинейные и квадратичные формы, страница 3

обозначим , числа  образуют квадратную матрицу порядка n:    которая называется матрицей Грама базиса е .

В силу свойств скалярного произведения

т.е. матрица  симметрична относительно главной диагонали. Такие матрицы называются симметрическими.

ЕслиX, Y – координатные столбцы векторов  в базисе е, то

(5.1)                                                                                      (5.2)

.

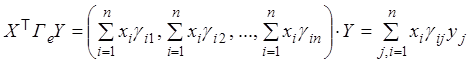Если  – ортонормированный базис, то

т.е. 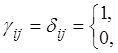             , отсюда получаем, что скалярное произведение векторов в ортонормированном базисе равно сумме попарных произведений соответствующих координат векторов (вспомнить произведение матриц).

5.3. Связь матриц Грама разных базисов

Пусть даны два базиса е и  f, связанные матрицей перехода T, т.е.  – координатные столбцы векторов  в базисах е и f соответственно, тогда :

       

Подставляя эти равенства в формулу (5.2) и используя тот факт, что , получаем

.

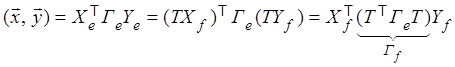С другой стороны , следовательно,

.                                                       (5.3)

Теорема 5.4. Определитель матрицы Грама любого базиса положителен ().

Доказательство. Рассмотрим формулу (5.3) в том частном случае, когда базис  является ортонормированным, тогда  и .

Вычислим детерминант обеих частей равенства, получим

, где .

Поскольку базис  произвольный, отсюда получаем требуемое.

Удобное представление матрицы Грама.

Пусть  базис в , тогда

таким образом

Теорема 5.5. Векторы  линейно зависимы тогда и только тогда, когда .

Доказательство.  Пусть система линейно зависима, тогда

    .

Умножая последовательно эту линейную комбинацию скалярно на векторы  , получим

   систему  однородных уравнений с  неизвестными  ().

В матричной записи:

.

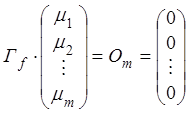Так как по условию , то существует нетривиальное решение этой системы линейных однородных уравнений, следовательно, определитель матрицы равен нулю, т.е. .

 Если , то по крайней мере один из столбцов матрицы  является линейной комбинацией остальных столбцов (смотри условия равенства нулю определителя матрицы), для определённости -й, т.е.

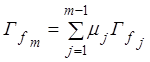, тогда      (), или 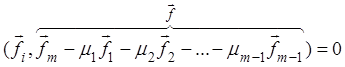                  (), т.е. вектор  ортогонален каждому из векторов . Но, с другой стороны,  – линейная комбинация этих векторов , следовательно, , что равносильно равенству  или 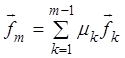, а это равносильно тому, что система векторов линейно зависима.

Теорема 5.6. Если векторы  линейно независимы, то .

Доказательство. Достаточно рассмотреть случай, когда  – базис, так как линейно независимая система векторов  является базисом своей линейной оболочки. Рассмотрим в линейной оболочке  ортонормированный базис , тогда (см. теорему 5.4) .

Пусть теперь оба базиса е и f ортонормированные, тогда  и формула (5.3) принимает вид

                                                          (5.4)

Определение. Матрица, удовлетворяющая условию (5.4) называется ортогональной.

Название обусловлено тем, что ортогональные матрицы и только они могут служить матрицами перехода от одного ортонормированного базиса к другому ортонормированному базису.

Будем обозначать ортогональные матрицы U, тогда

отсюда, транспонируя левую и правую части, получаем

, т.е.

                                                   (5.5)

По определению обратной матрицы: , сравнивая последние равенства, заключаем, что . Кроме того, матрица  тоже является ортогональной, так как и .

Вычислив определитель обеих частей равенства (5.5), получим , т.е. определитель ортогональной матрицы равен +1 или –1.

Обозначим , тогда

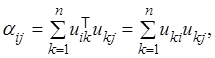
из 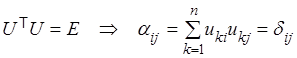, т.е. сумма квадратов элементов любого столбца (строки) ортогональной матрицы равна единице, а сумма попарных произведений соответствующих элементов различных столбцов (строк) равна нулю.

6. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВЫХ ПРОСТРАНСТВ

Все результаты, приведенные в предыдущих разделах, остаются в силе и для преобразований евклидовых пространств, но здесь есть скалярное произведение, что позволяет выделить некоторые очень важные классы преобразований.