Очевидно, что ![]() , так как ранг квадратичной формы по
определению равен рангу её матрицы в произвольном базисе, то из (7.11) и
условия
, так как ранг квадратичной формы по
определению равен рангу её матрицы в произвольном базисе, то из (7.11) и
условия ![]() :
: ![]() следует,
что ранг квадратичной формы равен
следует,
что ранг квадратичной формы равен ![]() (числу ненулевых
канонических коэффициентов):
(числу ненулевых
канонических коэффициентов): ![]() , так как
, так как ![]() .
.
Таким образом, число отличных от нуля канонических коэффициентов равно рангу квадратичной формы.
Из этого замечания следует, что число отличных от нуля канонических коэффициентов не зависит от выбора невырожденного преобразования, с помощью которого она приводится к каноническому виду.
Более того, при любом способе приведения к каноническому виду сохраняется число положительных и отрицательных канонических коэффициентов (закон инерции квадратичных форм).
Пусть
с помощью какого-либо невырожденного преобразования квадратичная форма (7.10)
приведена к виду (7.11), причём отличные от нуля коэффициенты занумерованы так,
что первые ![]() из них положительны, а остальные
из них положительны, а остальные ![]() отрицательны, т.е.
отрицательны, т.е.
![]() .
.
Рассмотрим ещё одно невырожденное преобразование координат (базиса) вида
 ,
, 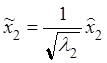 , …,
, …,  ,
, 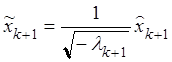 ,… ,
,… , 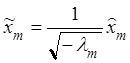 ,
, ![]() ,…,
,…, ![]() , что
равносильно записи
, что
равносильно записи ![]() , где
, где
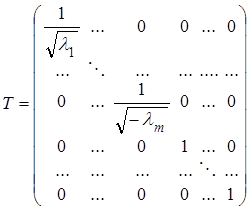 .
.
(легко видеть, что определитель этой матрицы отличен от нуля).
В результате этого преобразования квадратичная форма (7.10) примет вид
![]() (7.12)
(7.12)
который называется нормальным каноническим видом квадратичной формы.
Теорема 7.6. (Закон инерции квадратичных форм).
Число слагаемых с положительными (отрицательными) коэффициентами в нормальном каноническом виде квадратичной формы не зависит от способа приведения квадратичной формы к этому виду.
Доказательство.
Пусть квадратичная форма ![]() ранга
ранга ![]() двумя способами приведена к нормальному
виду и число положительных и отрицательных слагаемых в них различно, т.е.
двумя способами приведена к нормальному
виду и число положительных и отрицательных слагаемых в них различно, т.е.
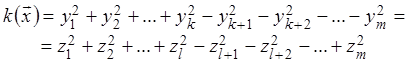 (*)
(*)
причём ![]() , а
, а ![]() ,
, ![]() –
координатные столбцы вектора
–
координатные столбцы вектора ![]() в канонических базисах
в канонических базисах ![]() ,
, ![]() .
.
Так
как переход от переменных ![]() к переменным
к переменным ![]() был невырожденным линейным
преобразованием, то и
был невырожденным линейным
преобразованием, то и ![]() будут выражаться через
будут выражаться через ![]() с помощью невырожденного линейного
преобразования, т.е.
с помощью невырожденного линейного
преобразования, т.е. ![]() ,
, ![]()
![]() и, следовательно,
и, следовательно,
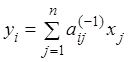 ,
(**)
,
(**)
где ![]() – элементы обратной матрицы
– элементы обратной матрицы ![]() .
.
Аналогично:
![]() ,
, ![]() и
и ![]() )
)
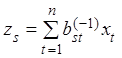 ,
(***)
,
(***)
где ![]() – элементы обратной матрицы
– элементы обратной матрицы ![]() .
.
Пусть,
для определённости ![]() , случай, когда
, случай, когда ![]() рассматривается аналогично. Запишем
систему равенств
рассматривается аналогично. Запишем
систему равенств
![]() ;
; ![]() (****)
(****)
Если левые части этих равенств
будут заменены их выражениями (**) и (***) через ![]() , то мы
получим систему
, то мы
получим систему ![]() линейных однородных уравнений с
линейных однородных уравнений с ![]() неизвестными
неизвестными ![]() .
.
Число
уравнений в этой системе меньше числа неизвестных (так как ![]() ), поэтому система имеет нетривиальное
решение (см. системы линейных уравнений)
), поэтому система имеет нетривиальное
решение (см. системы линейных уравнений) ![]() :
: ![]() .
.
Заменим
теперь в равенстве (*) все ![]() ,
, ![]() их выражениями из (**) и (***), тогда
получим:
их выражениями из (**) и (***), тогда
получим:
![]()
или
![]() , где символами
, где символами ![]() и
и ![]() обозначены
значения неизвестных
обозначены
значения неизвестных ![]() ,
, ![]() , получающиеся
при подстановке в (**), (***) вместо
, получающиеся
при подстановке в (**), (***) вместо ![]() решение
решение ![]() .
.
Из последнего равенства следует, что
![]() ,
, ![]() , так как левая часть
меньше либо равна 0, а правая часть больше либо равна 0.
, так как левая часть
меньше либо равна 0, а правая часть больше либо равна 0.
С
другой стороны, по самому выбору ![]() (см. (****))
(см. (****)) ![]() ,
, ![]() .
.
Таким
образом, система ![]() линейных однородных уравнений
линейных однородных уравнений ![]() , (
, (![]() ), которая
равносильна системе
), которая
равносильна системе ![]() с
с ![]() неизвестными
неизвестными
![]() , имеет нетривиальное решение
, имеет нетривиальное решение ![]() :
: ![]() ,
следовательно определитель матрицы системы равен 0 (см. системы линейных
уравнений)
,
следовательно определитель матрицы системы равен 0 (см. системы линейных
уравнений) ![]() , а это противоречит тому, что
преобразование (***) невырожденное, т.е.
, а это противоречит тому, что
преобразование (***) невырожденное, т.е. ![]() быть не
может.
быть не
может.
К
такому же противоречию мы придём и при ![]() .
.
Отсюда
следует, что ![]() . Теорема доказана.
. Теорема доказана.
Числа
![]() и
и ![]() называются
положительным и отрицательным индексами инерции квадратичной формы.
называются
положительным и отрицательным индексами инерции квадратичной формы.
Пусть
отрицательный индекс инерции равен ![]() , т.е.
, т.е.
![]() .
.
Теорема 7.7. (Необходимое и достаточное условие знакоопределённости квадратичной формы).
Квадратичная форма ![]() является знакоопределённой тогда,
когда - либо
является знакоопределённой тогда,
когда - либо ![]() , либо
, либо ![]() .
.
При этом, если ![]() , то форма положительно
определённая, если
, то форма положительно
определённая, если ![]() , то форма
отрицательно определённая.
, то форма
отрицательно определённая.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.