Полнота логических функций. Теорема дедукции. Свойства формальных теорий (логических систем). Равносильные формулы логики предикатов, страница 7

            0)&’)) - принцип математической индукции.

Теорема 1. Гёделя (о полноте)

Во всякой достаточно богатой теории (содержащей, например теорию Пеано) существует истинная формула, такая что нельзя доказать , что она выводима не её отрицание.

Теорема 2. Гёделя (о полноте)

Для всякой формальной теории достаточно богатой (содержащей, например формальную арифметику) формула доказывающая её непротиворечивость не может быть доказана средствами самой этой же теории.

Теория алгоритмов

Алгоритм – это некоторый свод правил, который через некоторое конечное количество шагов самопроизвольно приводит к правильному решению. (эти правила нельзя нарушать, иначе правильного ответа не будет) .

Требования предъявляемые к алгоритмам :

1.  Дискретность

а) Данных – разбитые на элементарные части не делимые дальше, изолированные друг от друга.

б) Действия – дробиться на элементарные шаги, далее на делимые, они сами по себе элементарные.

2. Детерменирование (определённость)

а) Данные б) Действия – при каждом элементарном шаге.

3. Результативность

Через конечное число элементарных шагов мы точно узнаем получили мы наше решение или нет.

4. Массовость

Решение задачи из большого числа однотипных задач.

Машина Тьюринга

Машина Тьюринга состоит из трёх частей :

1)  Память (лента) – в каждую ячейку записывается только один символ.

…

0

…

…

А={,...} - множество символов внешнего алфавита.

Пустой символ обозначается  0.

2)  Управляющие устройства – конечная совокупность некоторых состояний.

Q={} - совокупность символов внутреннего алфавита.

3) Головка – состоит только из одной ячейки, в некотором состоянии q обозревая символ a в             зависимости от данного состояния.

а) Затирает символ.

б) Пишет туда новый или тот же самый в) Сдвигается либо влево, либо вправо, либо остаётся на месте.

<>

D={} – положения

 - влево (L)

 - намести (E)

 - вправо (R)

Опр.

Совокупность команд  Р={<>} :

1)  Существует  – которое является заключительным, никогда .

2)   – никогда не может разветвляться на :

всегда сочетается с разными правыми частями (обеспечивает определённость наших действий) называется программой.

Машина Тьюринга – совокупность : <A,Q,P>

                                               где,  А - внешний алфавит.

                                                       Q - внутренний алфавит.      AQ=

Р – программа.

Машина Тьюринга точно описывает алгоритм.

Способы задания Машины Тьюринга

1)  Списком команд.

2)  Таблицы размерности  

На пересечении строки и столбца стоит .

3) В виде Орграфа.

Вершинами являются состояния.

На дуге пишется метка .

Опр.

Конфигурацией МТ называется следующая последовательность символов.

, где , А,  - слова,  последовательность символов из алфавита А.

Если , то .

Переходим в следующее состояние : (из одной конфигурации в другую)

<>

Опр.

Если существует , тогда говорят, что из   .

Опр.

Если .

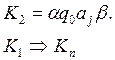
То говорят, что МТ переработала слово в слово :

Если не существует такого вывода, то МТ не может переработать данное слово.

Опр.

Две МТ называются эквивалентными друг к другу  :

1)  А=А₁=А₂ , их внешний алфавит совпадают.

2)   и  или и одновременно.

а) Либо перерабатывают слово.

б) Либо его не воспринимают.

Теорема

Существует такая МТ эквивалентная данной, которая на содержит направление на месте

Доказательство

Как её построить?

Есть такая команда : 

Можно сразу же написать :

Если , то

Иначе (= состояние «Стоп»)

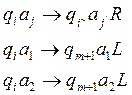
Опр.

            Если есть две МТ с совершенно не совпадающими внешними алфавитами, т.е.

            Тогда можно построить новую МТ :

 - заключительное состояние Машины (1)

- с учётом вышеперечисленных переделок.

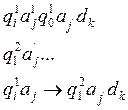      Команды склеиваются.

Опр.

Функция       – называется арифметической функцией, если