Полнота логических функций. Теорема дедукции. Свойства формальных теорий (логических систем). Равносильные формулы логики предикатов

§ 6.                                               Полнота логических функций.

Опр.

            Суперпозицией  над системой некоторых функций     

S={}

называется функция :

1)  Полученная из S переименованием переменных.

2)  Подстановкой в некоторую  вместо  переменной  некоторой функции .

Пр.

S={}  от переменных

, вместо подставим ()

, вместо подставим

, вместо  подставим .

Получается .

Опр.

Система булевых функций называется полной, если в некотором пространстве  (пространство логических функций  переменных) любая логическая функция  является суперпозицией функции из  :

S={}

Опр.

Базисом называется такая полная система в , если при потере некоторой функции она теряет свойство полноты.

Теорема Поста :

Система логических функций называется полной в ней существует некоторая функция    ;

;

;       

;

                                                              Классы Поста :

- класс функций сохраняющих ноль.

- класс функций сохраняющих единицу.

- класс самодвойственных функций.

- класс монотонных функций.

 монотонно возрастающая}

- класс линейных функций.

Опр.

Два двоичных набора  считаются частично упорядоченными, если все  :

Пр.

, - несравнимые.

Опр.

Логическая функция называется монотонно-возрастающей(убывающей), если

Опр.

Полиномом Жегалкина называется :

,

Таблица принадлежности некоторых функций Классам Поста

Функция
0	+			+	+
	+	+		+
	+				+
	+	+	+	+	+
	+				+
	+	+	+	+	+
	+				+
	+	+		+
		+			+
			+		+
		+
			+		+
		+			+
1		+		+	+

Пр.

1)    

0	0	0
0	1	0
1	0	0
1	1	1

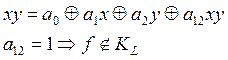
0	0	1
0	1	1
1	0	0
1	1	1

2)                                         

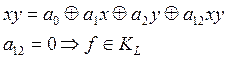
                                   - полная система.

Исчисления высказываний

Опр.

Формальной теорией называется система из 4-х множеств :

1) - алфавит.

2) Ф - множество букв (множество формул, т.е. слов)

3) А - множество аксиом (т.е. некоторых формул, носящих  специальные названия).

4) R – множество правил, т.е. некоторых операций над множеством формул :   .

Опр.

            Исчислением высказываний называется система из 4-х множеств : 

1) - множество символов (алфавит)

Символы :

1.1)   - пропозициональные элементы (переменные высказываний).

1.2)   -  логические связки.

1.3)  ( , ) – дополнительные символы.

2) – множество формул (слов)

Формулы :

2.1) Пропозициональные переменные (элементарные формулы)

2.2) Если  - формулы, то тогда - формулы.

3) - множество аксиом (формул особенного вида) :

a₁)

a₂)

a₃)

a₄)

a₅)

a₆)

a₇)

a₈)

a₉)

a₁₀)

a₁₁)

4)  R – множество правил вывода.

4.1) Правило подстановки

├

                                                                       ├

4.2) Правило отделения (modus ponens)

                                                           ├, ├

├

Опр.

Формула называется доказуемой в исчислении высказываний, если :

1)  Она аксиома.

2)  Получена по правилам вывода из доказуемых формул (├).

Опр.

Подстановка в формулу  вместо переменной  формулы  называется такая операция, что

1)  Если - пропозициональная переменная, то

1.a)  есть

1.b)  не есть 

2) Для формул   и - определены, тогда :

2.a) 

2.b) 

2.c) 

2.d) 

Пр.

Правило одновременной подстановки

Теорема 1

Если формула доказуема, то и доказуема формула полученная из неё путём подстановки вместо   в формулу

├

                                                                       ├                                                                                 Доказательство

Возьмем  пропозициональных переменных не содержащихся ни в формулу  ни в формулах . По правилу подстановки имеем :

В теореме дано, что - доказуема              ├

                                                                                  ├

С1

                       

По правилу подстановки :

├

                        ├     , применяя правило подстановки далее получаем :         ├

                                                                                                                                             ├

Применяя правило подстановки

 :                         ├