Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 14

Рис. 1.50.  Схема установки Рейнольдса.

Кроме того было установлено, что процесс перехода одного режима в другой не является полностью обратимым. Ламинарный режим переходит в турбулентный при значительно больших скоростях, чем скорости, при которых турбулентный режим переходит в ламинарный.

Ламинарный режим наблюдается при движении вязких жидкостей.

На основании анализа Рейнольдс предложил безразмерный критерий - число Рейнольдса:

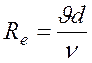,                                                                                  (68)

где:     - средняя скорость;

 - диаметр трубы;

 - кинематический коэффициент вязкости.

Число Рейнольдса является условием динамического пособия движущихся потоков жидкости, находящихся только под действием сил внутреннего трения и служит для характеристики потоков независимо от рода движущейся жидкости.

Критическая скорость - скорость, при которой происходит смена режимов движения.

Различают две критические скорости: верхнюю - 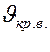 и нижнюю -, при этом  > .

Ламинарный режим переходит в турбулентный при 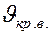, а турбулентный в ламинарный при .

Из выражения (68) критическая скорость:

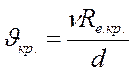, но с учетом того, что 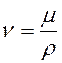получаем:

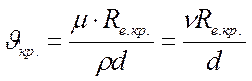^.                                                       (69)

Т.е. критическая скорость - прямо пропорциональна вязкости жидкости и обратно пропорциональна ее плотности и диаметру трубки.

Для трубопроводов работающих полным напором установлено, что:

R_{е кр.н.} = 2320, а R_{е кр.в.} = 13800.

Для трубопроводов работающих не полным напором или открытых русел, критическое Число Рейнольдса определяется по формуле:

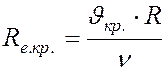,                                                                      (70)

где:  - гидравлический радиус.

Для них  

Определение режима движения имеет большое значение в практических расчетах.

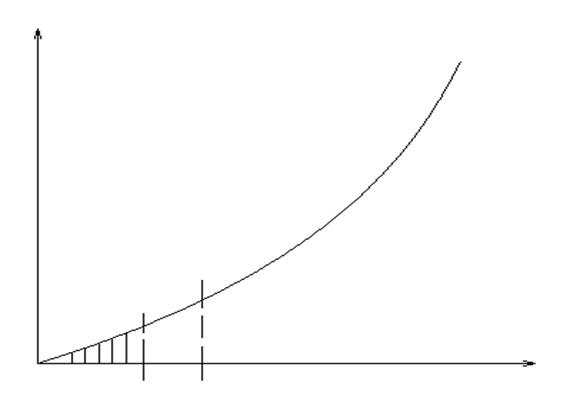
Опыты показывают, что потери напора  при ламинарном движении пропорциональны средней скорости течения, т.е. линейная связь:

,                                                                             (71)

где:  - коэффициент пропорциональности при ламинарном режиме (угловой коэффициент, АВ прямая).

В области турбулентного режима имеем:

,                                                                           (72)

где:     - параметр кривой (СД парабола);

 - показатель степени ().

Т.е. в  области турбулентного режима получаем квадратичную зависимость между  и .

 

Рис. 1.51.   График зависимости потерь напора от скорости.

В области ВС – переходная область (режим) используем выражение (1.72.), , точки В и С – критические точки.

На основании анализа установлен общий закон потерь энергии при движении жидкости.

Гидродинамическое подобие. Критерии подобия.

Полученное ранее число  имеет большое значение в гидравлике, так как является одним из основных критериев гидродинамического подобия.

Гидродинамическое подобие – это подобие потоков несжимаемой жидкости, включающей в себя подобия геометрические, кинематические и динамические (рис. 1.52.).

Геометрическое подобие – пропорциональность сходственных размеров и равенств углов, т.е. подобие русел.

Кинематическое подобие – это подобие линий тока и пропорциональность сходственных скоростей (обязательно геометрическое подобие русел).

Динамическое подобие – это пропорциональность сил, действующих на сходственные элементы кинематически подобных потоков.

Полное гидродинамическое подобие - соблюдение пропорциональности сил: давления, вязкости, тяжести.

Два потока считаются геометрически подобными, если между их линейными размерами L и l, площадями   и , объемами  и  соблюдаются соотношения:

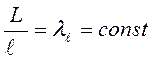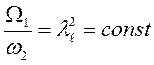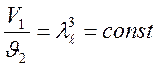; ; ;                (73)

где:  - линейный масштаб моделирования.

Две гидравлические системы будут кинематически подобными, если: а) траектории сходственных частиц геометрически подобны;