Ядерная физика: Учебно-методическое пособие для проведения практических занятий, страница 11

7.  При облучении толстой алюминиевой мишени пучком α-частиц с энергией  МэВ в результате реакции (α, n) испускается  нейтрон/с. Найти выход ω и среднее сечение σ данной реакции, если ток α-частиц равен  мкА.

8.  Бериллиевую пластинку облучают потоком нейтронов с энергией  МэВ, падающим нормально к ее поверхности. Оценить толщину пластинки, необходимую для η = 10 % воспроизводства нейтронов по реакции (n, 2n), сечение которой при данной энергии нейтронов  барн. Считать, что других процессов нет и вторичные нейтроны в пластинке не поглощаются.

Тема 5

Особенности кинематики ядерных реакций
для релятивистских частиц. Реакции с участием фотонов

Частица с массой m обладает энергией покоя E₀  = mc². Если частица начинает двигаться с некоторой скоростью u, то полная энергия  такой частицы будет больше ее энергии покоя на величину кинетической энергии, т. е.

,      (5.1)

где ,  - так называемый Лоренц-фактор. Из (5.1) кинетическая энергия движущейся частицы определяется следующим образом:

  (5.2)

В случае скоростей движения малых по сравнению с электродинамической постоянной c можно разложить  в ряд по степеням b: .

Если можно пренебречь всеми членами ряда кроме первых двух, т. е. если , то из (5.2) следует классическое выражение для кинетической энергии нерелятивистской частицы.

Часто удобнее использовать выражение для полной энергии релятивистской частицы, записанное в виде

,  (5.3)

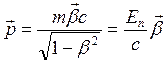,                                (5.4)

где  - вектор импульса релятивистской частицы.

Выражение (5.4) является инвариантом, т. е. сохраняется при переходе из одной инерциальной системы отсчета в другую.

Связь между кинетической энергией  и величиной импульса  релятивистской частицы получается из (5.3):

.         (5.5)

Законы сохранения импульса и энергии для ядерных реакций с участием релятивистских частиц имеют следующий вид:

,                                 (5.6)

,        (5.7)

где – импульсы налетающей частицы и мишени до взаимодействия; – импульсы частиц после взаимодействия;  – полные энергии частиц до взаимодействия;  – полные энергии частиц после взаимодействия.

Часто удобно массу частицы выражать в МэВ, а ее импульс в МэВ/с (здесь с – скорость света, а не секунда!).  В этом случае формулы (5.3) и (5.5) принимают вид

,                                            (5.8)

.                                          (5.9)

Пороговая кинетическая энергия частицы m, налетающей на неподвижную частицу M в реакции типа определяется выражением 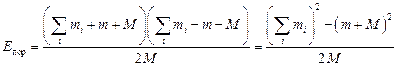(5.10).

.          (5.10)

Энергия реакции определяется выражением (5.11).

.                                 (5.11)

Тогда пороговая энергия с учетом энергии реакции запишется следующим образом:

.     (5.12)

Примеры

5.1. Вывести формулу (5.12).