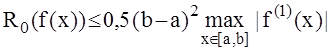Математика \ Вычислительная математика

Вычислительная математика: Методические указания к практическим и лабораторным работам, страница 4

 ,

поскольку интегрируемая функция f(x) заменяется на  = f(a).

В целях повышения точности интегрирования отрезок [a, b] можно разбить на n равных частей с шагом = (b - a)/n, вычислить площади элементарных прямоугольников, построенных на как на одной из сторон, и просуммировать их. В этом случае получаем обобщенную формулу прямоугольников

   , ,

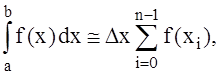
погрешность которой может быть оценена в виде

.

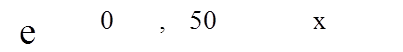 В общем случае представляя подынтегральную функцию f(x) в виде интерполяционного полинома Лагранжа  конечной степени m, получим квадратурные формулы Ньютона-Котеса

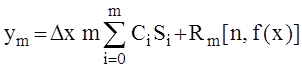,   m = 1, 2, ... ,7,

где

,  

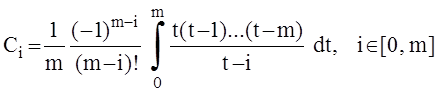- коэффициенты Котеса квадратурной формулы ,  а

,

причем  - дискретные отсчеты подынтегральной функции на интервале [a, b], разбитом на n подынтервалов с шагом = const,  - остаточный член или погрешность квадратурной формулы.

          Полагая m = 1, получим формулу трапеций

.

          При m = 2 имеем формулу парабол (n - число четное)

.

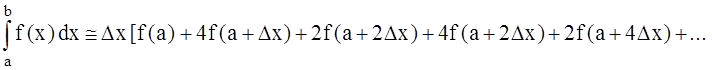
          Для рассматриваемых в лабораторной работе порядков m коэффициенты  и погрешности  квадратурных фомул Ньютона-Котеса имеют следующие значения:

где .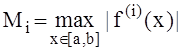

2. Подпрограммы, необходимые для выполнения работы

Подпрограмма

SUBROUTINE N1YINK (U,N,DT,M,F)

реализует квадратурные формулы Ньютона-Котеса порядка точности m Π[0, 7], причем подпрограмма функционирует таким образом, что количество отсчетов подынтегральной функции на [a, b] не зависит от величины m.

           Входные параметры подпрограммы:

           U(N) - N-мерный массив дискретных значений подынтегральной функции;

           N    - количество отсчетов подынтегральной функции на [a, b];

           DT   - шаг дискретизации подынтегральной функции;

           M    - порядок точности квадратурной формулы (M = m + 1);

           Выходные параметры подпрограммы:

           F    -  вычисленное значение интеграла.

Контрольные вопросы

1. Суть численного интегрирования посредством квадратурных формул

Ньютона-Котеса.

    2. Квадратурная формула прямоугольников.

    3. Квадратурная формула трапеций.

    4. Квадратурная формула парабол.

3. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Цель работы

          Практика использования итерационных методов решения системы линейных алгебраических уравнений. Сравнительный анализ методов.

Постановка задачи

          Решить систему линейных алгебраических уравнений (САУ)

,   ,   ,    

итерационными методами Зейделя и наискорейшего спуска с точностью до e = 0,001. Для сравнения с истинными значениями корней выполнить решение указанной САУ методом Гаусса.

Порядок выполнения работы

1. Ознакомиться с описанием работы. Уяснить цель и смысл задачи согласно варианту (см. табл. 3.1).

2. Записать в общем виде алгоритмы Зейделя и наискорейшего спуска.

3. Решить САУ с выводом результатов на каждой итерации методом Зейделя с начальными условиями  и   ,  .

4. Решить САУ с выводом результатов на каждой итерации методом наискорейшего спуска с начальными условиями  и   ,  .

5. Решить САУ методом Гаусса.

          6. Сравнить результаты, в том числе скорость сходимости итерационных алгоритмов.

          7. Оформить отчет.

Примечания:

1) пункты 3, 4, 5 выполняются по алгоритмам, реализованным в подпрограммах N1YTGA, N1YMGS, N1YMNS, N1YGAU, листинги которых приведены в приложении;

          2) в подпрограмме N1YGAU матрица A приводится к треугольной, т.е. исходная матрица A портится;

          3) при выполнении работы студенты должны составить головную программу, в которой необходимо осуществить:

          а) ввод данных,

          б) обращение к соответствующим подпрограммам N1YMGS и N1YMNS, в

которых выполняется только одна итерация, а окончание итерационной процедуры производить при выполнении условия

          Таблица 3.1

Скачать файл