Математика \ Вычислительная математика

Вычислительная математика: Методические указания к практическим и лабораторным работам, страница 13

          Метод наискорейшего спуска. Если функции fi(x), i Î[1, n], входящие в систему нелинейных уравнений являются непрерывными, вещественными функциями действительных переменных xi, i Î[1, n] и имеют непрерывные первые частные производные в области определения и только изолированные корни в этой области, то поиск решения такой системы можно свести к поиску минимума функционала

 ,

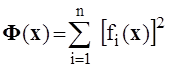причем спуск из некоторой точки xk функционала Ф(x) в сторону его минимума может осуществляться в виде

xk+1 = xk + hkvk , k = 0, 1, 2, ...,

где vk – вектор, задающий направление движения, а hk – параметр, обеспечивающий уменьшение значения функционала Ф(x) на данной итерации по сравнению с предыдущей.

          В качестве вектора vk выбирается

- grad Ф(xk) = ,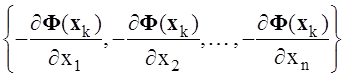

т.к. именно в направлении этого вектора Ф(x) убывает с максимальной скоростью.

          Параметр hk, вообще говоря, необходимо определять из условия уменьшения максимальным образом значения функционала Ф(xk+1) на (k + 1)–й итерации по сравнению с Ф(xk) на k–той итерации, что требует достаточно существенных вычислительных затрат, поэтому в лабораторной работе производится лишь приближенный выбор параметра hk в виде

hk = .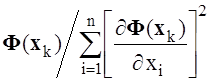

Таким образом, градиентный метод наискорейшего спуска определяется соотношением

xk+1 = xk –{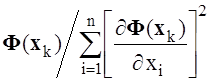}grad Ф(xk),  k = 0, 1, 2, ... .

          Окончание итерационной процедуры производится по условию

½Ф(xk+1) – Ф(xk)½ £ e

или

½grad Ф(xk+1)½ £ e,

где e > 0 – сколь угодно малое, наперед задаваемое число.

          Метод наискорейшего спуска уступает методу Ньютона в скорости сходимости и простоте реализации (большое количество вычислительных операций, связанных с неоднократным определением частных производных при вычислении вектора градиента), однако в данном случае решение системы уравнений может быть найдено при более грубых начальных условиях.

2. Подпрограммы, необходимые для выполнения работы

          Подпрограмма

SUBROUTINE  N1YIRU (NV, N, XI)

задает порядок и истинные значения корней системы нелинейных уравнений, а также записывает в файл ur.dat вид системы и ее корни.

          Входные параметры подпрограммы:

          NV – номер варианта.

          Выходные параметры подпрограммы:

          N – порядок системы уравнений;

          XI(N) – N–мерный вещественный массив корней системы.

          В подпрограмме

SUBROUTINE N1YNU (N, XI, DK, X)

по запросу вводится коэффициент, посредством которого производится затем реализация выбора начальных условий искомых корней системы.

          Входные параметры подпрограммы:

          N – порядок системы уравнений;

          XI(N) – N–мерный вещественный массив корней системы;

          DK – коэффициент, задающий начальные значения оценок искомых корней системы (вводится по запросу).

          Выходные параметры подпрограммы:

          X(N) – N–мерный вещественный массив начальных значений оценок искомых корней системы.

          Подпрограмма

SUBROUTINE N1YNTM (NV, N, X, EPS, NN, DF, F, DX, KM)

реализует метод Ньютона решения нелинейной системы алгебраических уравнений.

          Входные параметры подпрограммы:

          NV – номер варианта;

          N – порядок системы уравнений;

          X(N) – N–мерный вещественный массив начальных значений оценок корней системы уравнений;

          EPS – параметр останова.

          Промежуточные параметры:

          NN – параметр, определяющий количество частных производных нелинейных функций системы уравнений;

          DF(NN)– NN–мерный вещественный массив значений частных производных нелинейных функций системы уравнений;

          F(N) – N–мерный вещественный массив значений нелинейных функций системы уравнений;

          DX(N) – N–мерный вещественный массив значений приращений, уточняющих корни системы уравнений.

          Выходные параметры подпрограммы:

          X(N) – N–мерный вещественный массив найденных оценок корней системы уравнений;

Скачать файл