Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 18

      Шаг 4. Выполнить симплексное преобразование текущей таблицы с разрешающим элементом, выбранным на шаге 3б); объявить полученную таблицу и соответствующий базисный план  текущими.

      Шаг 5. Перейти к шагу 2.

       Двойственный симплекс-метод «выгодно» применять, когда  легко находится какая-нибудь симплексная таблица, удовлетворяющая условию оптимальности ( т. е. допустимая  таблица двойственной задачи).

       Пример 18.  Решить задачу ЛП

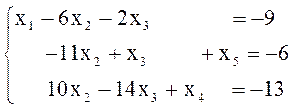
      Решение.  Здесь нет  «очевидных» начальных базисных переменных для применения обычного симплекс-метода; чтобы найти начальную таблицу, пришлось бы предварительно решить вспомогательную задачу (см. п. 5). Заметим, что  выражение  F  содержит только две переменные,  , причем обе с отрицательными  коэффициентами, -3   и -2. Выбрав  за свободные ( тогда

- базисные), получим симплексную таблицу  удовлетворяющую условию оптимальности  – элементами строки  F  будут положительные числа 3 и  2. Чтобы найти остальные элементы  , надо разрешать систему ограничений относительно

 в данной задаче эти переменные выражаются через   непосредственно из 1-го, 3-го  и 2-го уравнений соответственно. Используя   в  качестве начальной, применим двойственный симплекс-метод.

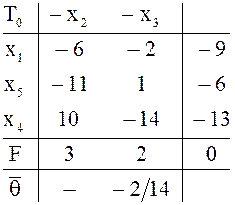
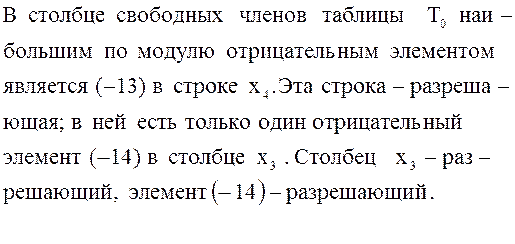                                     Выполнив симплексное преобразование   , получим таблицу .

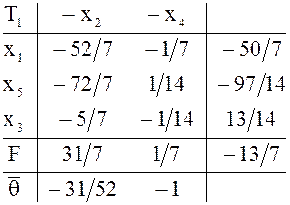
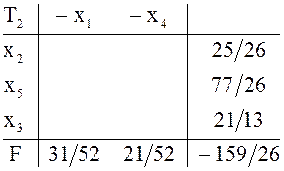
В   разрешающая строка  Наибольшее по модулю двойственное симплексное отношение  () указывает  на разрешающий столбец   При переходе от  вычисляем сначала элементы столбца свободных членов. Так как все они оказались неотрицательными,  не только удовлетворяет условию оптимальности, как все предыдущие, но и допустима. По критерию  оптимальности 

 - единственный оптимальный план , 

      Типичными примерами задач с очевидной начальной таблицей для двойствен ного симплекс-метода  являются задача о диете  (7) – (9) и задача о раскрое.

      Пример 19. Листы материала размером   надо раскроить так, чтобы получились заготовки двух типов: 800 штук заготовок размером  и 400 штук заготовок размером  Как получить необходимое число заготовок  с минимальным расходом материала?

     Решение. В условиях задачи способ раскроя листа полностью определяется парой чисел   где  количества получающихся заготовок размеров    и   соответственно. Для получения необходимого числа заготовок из минимального числа листов можно использовать только «не улучшаемые» способы раскроя, т. е.  такие, для которых раскрои вида   невозможны. Легко проверяется, что таких способов раскроя имеется всего четыре: (3, 1),  (2, 6), (1,9) и (0, 13),

 ЧЕРТЕЖ

     Пусть    число листов, раскроенных этими четырьмя способами. Тогда  расход материала (в листах), а    и 

- количества полученных заготовок размеров   и  Моделью задачи о раскрое будет следующая задача ЛП:

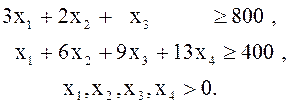
Каноническая форма этой задачи имеет вид

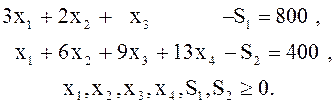
Таблица   с базисными переменными    удовлетворяет  условию оптимальности и применение двойственного симплекс-метода дает цепочку  таблиц 

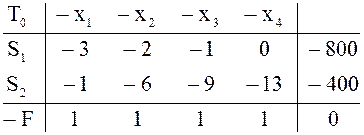
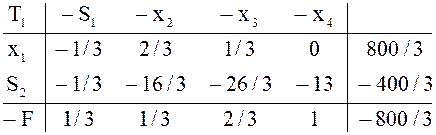
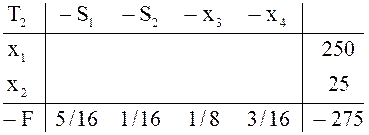
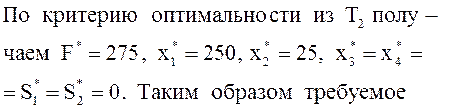
число заготовок можно получить из 275 листов, раскроив 250 из них первым способом  и  25 – вторым способом. 

      В заключение выясним экономический смысл  оптимальных значений переменных двойственной задачи  (31) – (33) в случае, когда прямая задача  (14) – (17) рассматривается как модель   задачи о ресурсах. Напомним,что  в этом случае правые части   ограничений прямой задачи (эти же числа – коэффициенты целевой функции   двойственной задачи) представляют собой запасы ресурсов, а величина   максимально возможный доход от реализации всей произведенной продукции. Предположим, что    единственный оптимальный план двойственной задачи. Из первой теоремы двойственности следует, что