Эти теоремы показывают, что при решении задач ЛП фактически можно рассматривать только опорные планы, а не все допустимые. В примерах 7 – 9 рассматривались изменения значений целевой функции и базисных переменных при возрастании одной из свободных переменных. Из анализа этих изменений ясно, как надо выбирать разрешающий элемент «текущей» симплексной таблицы, чтобы улучшить соответствующий опорный план, и как определить, получен ли уже оптимальный план и существуют ли вообще оптимальные планы. Такое последовательное улучшение опорных планов - главная идеяосновного алгоритма численного решения задач ЛП, получившего название симплекс-метода.
Для применения симплекс-метода задачу ЛП надо привести к каноническому виду (см. п.2). Кроме того, предполагается, что уже найдена одна из допустимых
симплексных таблиц – начальная симплексная таблица. Ниже будет показано, как можно найти такую таблицу или установить, что задача ЛП не имеет допустимых планов.
Алгоритм симплекс-метода
Шаг 1. Объявить начальную симплексную таблицу и соответствующий опорный план текущими.
Шаг 2 (Проверка оптимальности). Просмотреть строку F текущей таблицы (кроме свободного члена).
а) Если в строке F нет
отрицательных элементов (все ![]() , то текущий опорный
план – оптимальный; если при этом нет и нулевых элементов, то оптимальный план
- единственный, если нулевые элементы есть, то множество оптимальных планов
бесконечно.
, то текущий опорный
план – оптимальный; если при этом нет и нулевых элементов, то оптимальный план
- единственный, если нулевые элементы есть, то множество оптимальных планов
бесконечно.
б) Если в строке F есть отрицательные элементы, выбрать среди них наибольш ий по модулю и объявить соответствующий столбец разрешающим.
Шаг 3 (Выбор разрешающего элемента). Просмотреть разрешающий столбец текущей таблицы (кроме элемента строки F).
а) Если в разрешающем столбце нет положительных элементов (все ![]() , то целевая функция не ограничена и
оптимальных планов нет.
, то целевая функция не ограничена и
оптимальных планов нет.
б) Если в разрешающем столбце есть положительные элементы, то для всех содержащих
эти элементы строк вычислить и записать в столбец ![]() отношения
свободных членов таблицы к соответствующим элементам разрешающего столбца -симплексные
отношения (в строках, содержащих нулевые или отрицательные элементы
разрешающего столбца, если такие имеются, вместо симплексных отношений
поставить прочерки). Строку с минимальным симплексным отношением
объявить разрешающей, элемент на пересечении разрешающей строки с разрешающим
столбцом объявить разрешающим.
отношения
свободных членов таблицы к соответствующим элементам разрешающего столбца -симплексные
отношения (в строках, содержащих нулевые или отрицательные элементы
разрешающего столбца, если такие имеются, вместо симплексных отношений
поставить прочерки). Строку с минимальным симплексным отношением
объявить разрешающей, элемент на пересечении разрешающей строки с разрешающим
столбцом объявить разрешающим.
Шаг 4 (Улучшение плана). Выполнить симплексное преобразование текущей таблицы с разрешающим элементом, выбранным на шаге 3б); объявить полученную таблицу и соответствующий опорный план текущими.
Шаг 5. Перейти к шагу 2.
Результатом применении симплекс-метода будет цепочка допустимых симплексных
таблиц ![]() и соответствующих опорных планов
и соответствующих опорных планов ![]() такая, что
такая, что ![]() В
большинстве задач ЛП значения целевой функции
В
большинстве задач ЛП значения целевой функции ![]() строго возрастают и решение задачи завершается через конечное
число шагов на таблице, удовлетворяющей требованиям шага 2а) или шага
3а). Особые случаи всегда связаны с вырожденностью решаемой
задачи. Задача ЛП называется вырожденной, если у нее есть опорные планы,
в которых кроме всех свободных переменных равны нулю и некоторые
базисные. Разберем подробно простейший из таких особых случаев.
строго возрастают и решение задачи завершается через конечное
число шагов на таблице, удовлетворяющей требованиям шага 2а) или шага
3а). Особые случаи всегда связаны с вырожденностью решаемой
задачи. Задача ЛП называется вырожденной, если у нее есть опорные планы,
в которых кроме всех свободных переменных равны нулю и некоторые
базисные. Разберем подробно простейший из таких особых случаев.
Пример 10. Решить симплекс-методом задачу ЛП ![]() с
ограничениями
с
ограничениями ![]()
Решение. Начальная таблица ![]() находится так же, как
в предыдущих примерах. Одна из возможных цепочек состоит из трех таблиц:
находится так же, как
в предыдущих примерах. Одна из возможных цепочек состоит из трех таблиц: ![]()


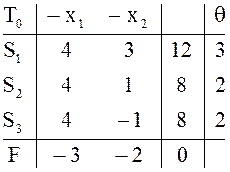
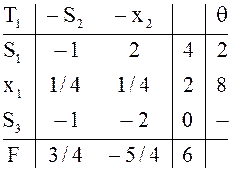
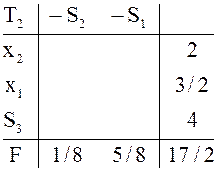
Начальной таблице ![]() соответствует опорный план
соответствует опорный план ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.