Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 16

Ограничения и целевая функция  прямой задачи  «записаны» в строках таблицы 5, ограничения и целевая функция двойственной задачи «читаются» по столбцам. Ограничению с номером   прямой задачи соответствует переменная   двойственной; переменной   прямой задачи -  ограничение двойственной.

  Пример 15. Записать условие  задачи, двойственной к стандартной  задаче из примера 11.

     Решение. Воспользуемся схемой из таблицы 5. Рядом с ограничениями каждой из  задач записаны в скобках соответствующие переменные другой задачи:

     Двойственную задачу примера 15 можно привести к стандартному виду, затем записать условие двойственной к ней и снова привести к стандартному виду. Проверьте, что результатом таких преобразований будет исходная (прямая) задача. Нетрудно понять, что и в общем случае задача, двойственная к двойственной совпадает с исходной. Поэтому  прямую и двойственную задачи называют также взаимодвойственными  или  двойственной парой.

В теории ЛП доказаны следующие утверждения (теоремы двойственности), устанавливающие связи между свойствами задач двойственной пары.

     Теорема 1. Если одна из  задач двойственной пары разрешима, т. е имеет оптимальные планы, то разрешима и другая задача. При этом для оптимальных планов имеет место равенство  . Для разрешимости одной (а, значит, и другой) задачи необходимо и достаточно, чтобы каждая из них имела хотя бы один допустимый план.

     Теорема 2. Для того, чтобы допустимые планы  

пары двойственных задач (14) – (16) и (31) – (33) были их оптимальными планами, необходимо и достаточно, чтобы они удовлетворяли системе уравнений

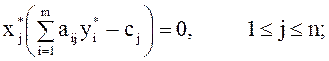
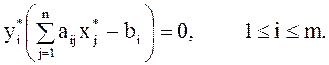
   Теорема 1 – центральный результат всей теории ЛП. Теорема 2 позволяет найти оптимальный план одной из задач двойственной пары по оптимальному плану другой.

     Пример 16. Решить задачу ЛП

                                                  ,

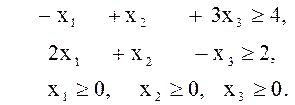
     Решение.  Запишем условие двойственной задачи

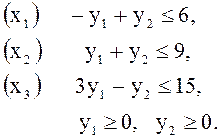
Эту задачу можно решить графически (проделайте самостоятельно), в результате получим   По теореме 1 исходная (прямая) задача также имеет оптимальный план   Чтобы найти   подставим 

 в систему уравнений из теоремы 2:

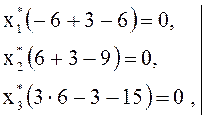
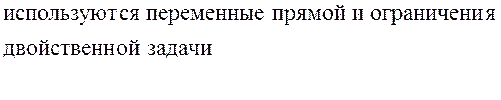
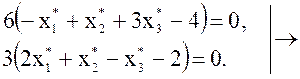
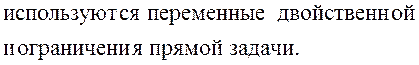
Второе и третье  уравнения представляют собой тождества 0 =  0. Из остальных уравнений находим единственный оптимальный план исходной задачи                                      

 Для определения   даже не обязательно подставлять эти числа в выражение для целевой функции  F, так как из теоремы 1 следует  (проверьте подстановкой).

     В разобранном примере  решалось более «легкая» из пары двойственных задач, ответ другой задачи получался после решения системы линейных уравнений. В случае , когда оптимальный план одной из задач находится симплекс-методом, оптимальный план другой можно найти непосредственно по заключительной симплексной таблице без дополнительных вычислений.    

     Пример 17. Приведем обе задачи двойственной пары из предыдущего примера к канонической форме. В прямой задаче заменим   и введем балансовые переменные  в двойственной задаче введем балансовые переменные            

     Примем за базисные переменные   в прямой  задаче  (тогда  свободные) и переменные   в двойственной задаче  (тогда  свободные). Каждая базисная переменная  , содержатся в определенном ограничении  одной  из задач двойственной  пары; этому ограничению соответствует определенная  свободная  переменная другой задачи. Это позволяет установить следующее соответствие между переменными  взаимодвойственных задач: