Разработка математической модели технологического процесса с применением метода центральных композиционных ортогональных планов, страница 5

Изменяем с определенным шагом значение , вычисляем Х₁ и Х₂, подставляем их в уравнение регрессии в кодированном виде пока не получим желаемый результат.

С помощью метода Ридж - анализа получаем оптимальный режим в кодированном виде, затем осуществляем перевод в натуральный вид по формуле:

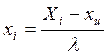,                                                                                                                        (27)                                                                                                                       

Из уравнения регрессии в каноническом виде берутся исходные данные в методе движения вдоль канонических осей. В соответствии с поставленной задачей в канонической системе координат выбирают ось, вдоль которой параметр оптимизации изменяется в желаемом направлении с максимальной скоростью: если необходимо найти максимальное значение параметра оптимизации движение происходит вдоль положительной оси, если минимальный – по отрицательной. Задаваясь различными значениями параметра оптимизации, вычисляем соответствующие им режимы и подвергаем их опытной проверки. В связи с симметрией поверхности каждому значению параметра опти­мизации соответствуют два режима. Поиск оптимального режима без исследования поверхности отклика обычно даёт возможность выделить только один оптимальный режим. Причём исследователь даже не подозревает о существовании второго режима, который может оказаться более эффективным для технологии.

Для получения у_мах должно выполняться условие , выбираем  положительную ось по которой быстрее придем к оптимуму, движемся по Х₁, стабилизируя второй фактор на центральном уровне (Х₂=0).

Уравнения регрессии в каноническом виде принимает следующий вид: >у_s=В₁₁х₁² − выражаем Х_i:

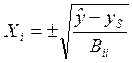,                                                                                       (28)

В место  подставляем желаемый результат и получаем два оптимальных режима:

Первый режим            Х₁=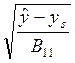,                                                                                           (29)

Второй режим                   Х₂=−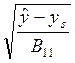,                                                (30)

Значения факторов получили в каноническом виде, перевод факторов в кодированный вид осуществляем по формулам (20).

Далее производим перевод значений факторов в натуральный вид по формуле (27).

1.3 Входная и выходная информация

Таблица 4 - Входная и выходная информация

2 Результаты расчётов и  выводы

2.1 Анализ качества полученной математической модели

Для построения матрицы планирования за основу берётся план первого порядка n=2⁴. 16 строк мат­рицы и соответственно столбцы х_i и х_iх_j заполняются чередованием +1 и -1 по формуле 2^k-1 и перемножением столбцов.

К точкам ПФЭ планов 1 порядка добавляем 2к звездных точек, расположенных на ко­ординатных осях факторного пространства на одинаковых расстояниях ±α от центра плана. Звездное плечо для k=4 равно α=1,41. Заполняем 8 строк матрицы (с 17 по 24), используя значение звездного плеча.