![]() и
и ![]() . Если
. Если ![]() , то буквы
, то буквы ![]() и
и ![]() несовместимы
и для всякой конъюнкции ЭНФ, содержащей букву
несовместимы
и для всякой конъюнкции ЭНФ, содержащей букву ![]() ,
найдется конъюнкция, которую можно получить из первой путем замены
,
найдется конъюнкция, которую можно получить из первой путем замены ![]() на
на ![]() . Отсюда
следует, что
. Отсюда
следует, что ![]() и
и
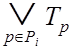
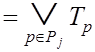 . (3.16)
. (3.16)
|
Отношение между контактами |
Отношение между неисправностями |
|
|
|
|
|
|
|
|
|
|
|
|
Из (3.10) и (3.16) имеем: ![]() , то есть
, то есть ![]()
![]() . В этом случае контакты
. В этом случае контакты ![]() и
и ![]() включены
параллельно и их отказы типа «короткое замыкание» эквивалентны. В схеме рис.
3.1 имеем:
включены
параллельно и их отказы типа «короткое замыкание» эквивалентны. В схеме рис.
3.1 имеем: ![]()
![]() ,
, ![]()
![]() .
.
Пусть ![]()
![]() ,
, ![]()
![]() . Тогда
. Тогда ![]() = {1,
2},
= {1,
2}, ![]() = {3, 4} (см. формулу (3.3)) и
= {3, 4} (см. формулу (3.3)) и
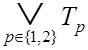
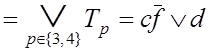 .
.
Если ![]() , то буквы a и b несовместимы
и для всякой конъюнкции ЭНФ, содержащей букву a, найдется конъюнкция,
содержащая букву b
и все буквы, составляющие первую конъюнкцию (кроме a), а также некоторое
множество других букв. Отсюда следует, что
, то буквы a и b несовместимы
и для всякой конъюнкции ЭНФ, содержащей букву a, найдется конъюнкция,
содержащая букву b
и все буквы, составляющие первую конъюнкцию (кроме a), а также некоторое
множество других букв. Отсюда следует, что ![]() и
и
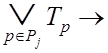
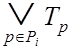 . (3.17)
. (3.17)
Из (3.10) и (3.17) имеем: ![]() , то есть
, то есть ![]() . В
схеме рис. 3.1:
. В
схеме рис. 3.1: ![]() ,
, ![]() . Пусть
. Пусть ![]() ,
, ![]() . Тогда
. Тогда
![]() ,
, ![]() и
и
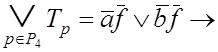
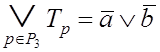 .
.
Из соображений двойственности
следует: 1) если ![]() , то
, то ![]() ; 2) если
; 2) если ![]() , то
, то ![]() . В схеме рис. 1.3 имеем:
. В схеме рис. 1.3 имеем: ![]() ,
, ![]() ,
, ![]() . Поэтому
. Поэтому ![]() ,
, ![]() ,
, ![]() .
.
Рассмотренные отношения между неисправностями отдельных контактов обобщаются на случай произвольных кратных неисправностей контактов следующей теоремой [26].
Теорема 3.1. Для
того, чтобы ![]() достаточно одновременного выполнения
следующих условий:
достаточно одновременного выполнения
следующих условий:
1) ![]() ;
;
2) ![]() ;
;
3) ![]()
![]() ;
;
4) ![]()
![]() .
.
Доказательство. Так
как ![]() (3.9), то достаточно доказать справедливость
импликаций
(3.9), то достаточно доказать справедливость
импликаций
![]() и
и ![]() . (3.18)
. (3.18)
Достаточно доказать только одну из импликаций (например,
вторую), так как условия теоремы двойственны относительно ЭНФ и ОЭНФ. Функции ![]() рассчитываются по формуле (3.10). Покажем,
что
рассчитываются по формуле (3.10). Покажем,
что
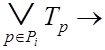
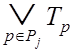 , (3.19)
, (3.19)
откуда из (3.10) следует (3.18).
![]() ,
, ![]()
и существуют отношения: ![]() ,
, ![]() , ... ,
, ... , ![]() ,
, ![]() , ... ,
, ... ,
![]() . Рассмотрим конъюнкцию
. Рассмотрим конъюнкцию ![]() , где
, где ![]() – часть
конъюнкции, состоящая из букв
– часть
конъюнкции, состоящая из букв ![]() . Чтобы доказать (3.19),
надо показать, что
. Чтобы доказать (3.19),
надо показать, что
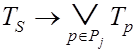 ,
(3.20)
,
(3.20)
где ![]() –
функция, реализуемая конъюнкцией
–
функция, реализуемая конъюнкцией ![]() .
.
Пусть ![]() , где
, где ![]() ,
, ![]() . Так как
. Так как ![]() , то на
основании свойства этого отношения букв можно утверждать, что в ЭНФ существует
конъюнкция
, то на
основании свойства этого отношения букв можно утверждать, что в ЭНФ существует
конъюнкция ![]() такая, что
такая, что ![]() . Знак
включения означает здесь, что конъюнкция
. Знак
включения означает здесь, что конъюнкция ![]() является
частью конъюнкции
является
частью конъюнкции ![]() . Пусть
. Пусть ![]() ,
где
,
где ![]() ,
, ![]() ,
, ![]() . Тогда в ЭНФ входит конъюнкция
. Тогда в ЭНФ входит конъюнкция ![]() . Так как
. Так как ![]() , то в
ЭНФ существует конъюнкция
, то в
ЭНФ существует конъюнкция ![]() такая, что
такая, что ![]()
![]() . Пусть
. Пусть ![]()
![]() , где
, где ![]() ,
, ![]() ,
, ![]() . Тогда в ЭНФ входит конъюнкция
. Тогда в ЭНФ входит конъюнкция ![]() . Продолжая аналогичные рассуждения
относительно всех букв, связанных отношением
. Продолжая аналогичные рассуждения
относительно всех букв, связанных отношением ![]() ,
получаем, что в ЭНФ входит конъюнкция
,
получаем, что в ЭНФ входит конъюнкция ![]() , где
, где ![]() . Так как
. Так как ![]() , то на
основании свойства отношения замены можно утверждать, что в ЭНФ существует конъюнкция
, то на
основании свойства отношения замены можно утверждать, что в ЭНФ существует конъюнкция
![]() . Аналогично, так как
. Аналогично, так как ![]() , то существует конъюнкция
, то существует конъюнкция ![]() . Обозначим ее через
. Обозначим ее через ![]() .
.
Покажем теперь, что ![]() . Для этого достаточно показать, что
неисправность
. Для этого достаточно показать, что
неисправность ![]() не фиксирует в 0 буквы
конъюнкции
не фиксирует в 0 буквы
конъюнкции ![]() . Предположим обратное, т.е. что среди букв
конъюнкции
. Предположим обратное, т.е. что среди букв
конъюнкции ![]() существует буква
существует буква ![]() ,
которая фиксируется в 0 неисправностью
,
которая фиксируется в 0 неисправностью ![]() и, следовательно,
и, следовательно,
![]()
![]() . Тогда буквы
. Тогда буквы ![]() , входящие в множество
, входящие в множество ![]() , совместимы с буквой
, совместимы с буквой ![]()
![]() . С другой стороны,
буква
. С другой стороны,
буква ![]() не находится в отношении эквивалентности с
буквами множества
не находится в отношении эквивалентности с
буквами множества ![]() , так как
, так как ![]()
![]()
![]() и
и ![]() (в противном случае в конъюнкцию
(в противном случае в конъюнкцию ![]() входила бы буква
входила бы буква ![]() ).
Таким образом, принятое предположение противоречит четвертому условию теоремы.
).
Таким образом, принятое предположение противоречит четвертому условию теоремы.
Итак, ![]() и поэтому имеем
и поэтому имеем
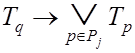 , (3.21)
, (3.21)
где ![]() – функция, реализуемая конъюнкцией
– функция, реализуемая конъюнкцией ![]() .
.
Так как ![]() , то
, то ![]()
![]() , откуда из (3.21)
следует (3.20). Теорема доказана.
, откуда из (3.21)
следует (3.20). Теорема доказана.
Рассмотрим две неисправности схемы (рис. 3.11)
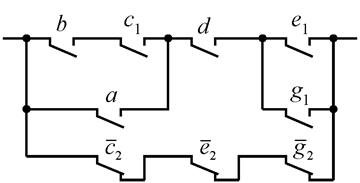
Рис.3.11. Пример контактной схемы
![]() и
и ![]()
![]() . Матрица совместимости
схемы показана в табл. 3.12, а ее ЭНФ и ОЭНФ имеют вид:
. Матрица совместимости
схемы показана в табл. 3.12, а ее ЭНФ и ОЭНФ имеют вид:
![]() ,
,
![]()
![]()
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.