Теория контроля контактных схем, страница 12

          Доказательство. Рассмотрим пять возможных видов неисправностей кратности четыре: (), (), (), (), (). Из теоремы 4.1 следует, что  () и  (). Для анализа других видов неисправностей введем двоичный вектор совместимости пар контактов, который имеет в данном случае шесть разрядов (табл. 3.15). Всего, таким образом, существует 64 случая отношений совместимости между четырьмя контактами. Рассмотрение всех этих случаев для неисправностей () и () показывает, что всегда найдется одиночная неисправность, которая находится, согласно теореме 3.1, в отношении эквивалентности или включения с данными неисправностями. Анализ неисправности () показывает, что существуют восемь двоичных векторов, представленных в табл. 3.15, для которых условия теоремы 3.1 не выполняются. Общим для этих векторов является то, что каждый контакт из множества  совместим только с одним контактом из множества , причем с другим, чем тот, с которым совместим второй контакт из множества  (см. условия 2 и 3 теоремы). Теорема доказана.

                                                                                      Т а б л и ц а   3.15

          Доказанная теорема определяет условия, когда неисправность четырех контактов не обнаруживается любым одиночным тестом. Ее условия являются достаточно жесткими и резко сокращают список неисправностей  кратности  четыре,  которые  необходимо  рассматривать   при   построении   полного   проверяющего   теста.  В схеме (рис. 3.12) всего существует 1120 неисправностей. Из них только 10 удовлетворяют всем условиям теоремы 3.3:  = , , , , , , , , , .

          Поясним физический смысл условий теорем 3.2 и 3.3. Предположим, что в контактной схеме присутствует неисправность . Для ее компенсации (маскировки) необходимо наличие неисправности  несовместимого с  контакта  (см. рис. 3.13,а). Но поскольку обратной компенсации нет, неисправность кратности два () обнаруживается на наборах, обнаруживающих . Поэтому, . Чтобы в данном случае компенсировать , необходимо наличие неисправности  совместимого с  контакта  (см. рис. 3.13,б).

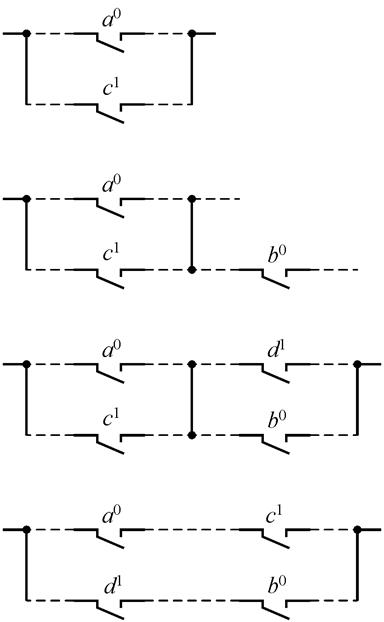
Рис.3.13. Маскировка неисправностей

 Но при этом нет компенсации неисправности  и поэтому (). Чтобы компенсировать , необходимо наличие  неисправности    несовместимого  с    контакта  (см. рис. 3.13, в). Поскольку неисправность  может быть компенсиро-вана неисправностью , получена структура неисправности кратности четыре, которая может компенсировать каждую одиночную составляющую ее неисправность хотя бы на одном проверяющем наборе. Следовательно, она может быть не обнаружена хотя бы одним одиночным проверяющим тестом. Структура полученной неисправности соответствует условиям теоремы 3.3. Другая возможная структура приведена на рис. 3.13, г.

          Результаты, аналогичные теореме 3.3 могут быть сформулированы и для неисправностей кратности пять и более. В общем же случае имеет место следующая теорема [17].

          Теорема 3.4. Для того чтобы неизбыточная неисправность  кратности  содержалась в контрольном списке , необходимо выполнение следующих условий:

          1) неисправность  содержит как составляющую хотя бы одну неисправность кратности четыре, удовлетворяющую условиям теоремы 3.3;

2);

3).