Другие предметы \ Беспроводные линии связи и сети

Блочные коды с коррекцией ошибок, страница 6

Описанный код известен как код исправления однобитовых ошибок (single-error-correcting — SEC). Одной из разновидностей этого кода является код ис­правления 1-битовых и обнаружения 2-битовых ошибок (single-error-correcting, double-error-detecting — SEC-DED). Как показано в табл. 8.1, для таких кодов требуется на один бит больше, чем для кодов SEC. Этот дополнительный бит яв­ляется битом четности для всего кодового блока.

Циклические коды

     Большинство используемых на практике блочных кодов с коррекцией ошибок
относятся к категории циклических. Для циклических кодов справедливо следующее: если n - битовая последовательность с= (с0, с1,..., сn-1) является кодовым
словом, то последовательность (сn-1, c0, с1… сn-2), полученная с помощью циклического сдвига с на одну позицию вправо, также используется в качестве кодового слова. Данный класс кодов можно легко кодировать и декодировать с использованием линейных регистров сдвига с обратной связью (linear feedback shift register — LFSR). Примерами циклических кодов являются коды Боуза-Чоудхури-Хокве нгема (БХЧ) и коды Рида-Соломона.

     Реализация циклического кодера как регистра LFSR подобна реализации, для кодов обнаружения ошибок. Основное отличие со­стоит в том, что вход кода CRC имеет произвольную длину и в результате получается контрольный код CRC фиксированной длины, тогда как циклический код с коррекцией ошибок генерирует контрольный код (n-k бит) на основе входной последовательности фиксированной длины (k бит).

     На рис. 3 представлена реализация в виде LFSR декодера циклического блочного кода. Отметим, что в кодере k бит данных используются как вход для полу­чения в регистре сдвига кода длиной (n-k) бит. Для декодера входом являются полученные n бит, которые содержат k бит данных, за которыми следуют (n-k) контрольных битов. При отсутствии ошибок после первых к тактов регистр сдви­га содержит последовательность контрольных битов, идентичную переданной. После оставшихся (n-k) тактов регистр сдвига будет содержать код-синдром.


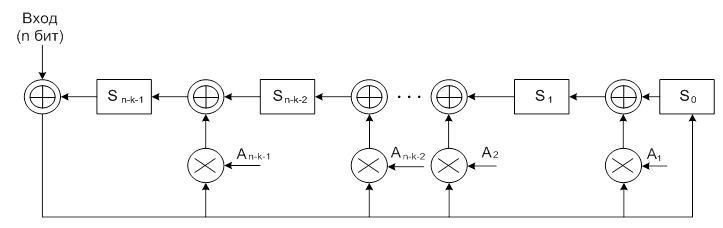
Рис.3 Генератор блочного синдрома для делителя

1 + A1X + A2 X2 +... + Аn-1   Xn-k-1+Xn-k

     Для декодирования циклического кода используется следующая процедура.

1. С помощью полученных битов вычисляется код-синдром. Вычисления про­водятся аналогично тому, как кодер обрабатывает биты данных для полу­чения контрольного кода.

2. Если все биты синдрома равны нулю — ошибки отсутствуют.

3. Если  синдром  отличен от нуля,  производится дополнительная  обработка для исправления-ошибки.

     Значение синдромов можно понять, изучив блочный код с использованием полиномов. Как и при проверке четности с избыточностью, конкретный циклический код можно представить полиномиальным делителем, именуемым порож­дающим многочленом (или генератором). Для кода (n,k) порождающий много­член можно записать в таком виде:

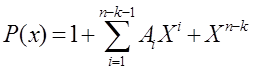
где каждый из коэффициентов Ai может принимать значения 0 или 1, что соответствует двоичному разряду в делителе. Например, для Р= 11001 многочлен Р(Х) имеет вид X4 + X3 + 1. Аналогично последовательность битов данных представляется полиномом D(X), а контрольный код — полиномом С(Х).  Контрольный код определяется следующим образом.

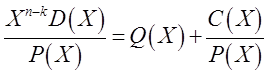
Т.е. блок данных D(X) сдвигается влево на (n-k) бит и делится на Р(Х). В результате получим частное Q(X) и остаток С(Х) длиной (n-k) бит. Передаваемый блок — это конкатенация D(X) и С(Х):

Т(Х) = Xn-k  D(X) + С(Х).       

      При отсутствии ошибок передачи Т(Х) должно делиться на Р(Х) без остатка, что легко продемонстрировать:

                                             

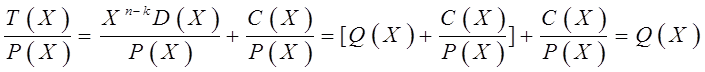
     Последнее выражение справедливо в соответствии с правилами арифметики по модулю 2 (а + а = 0). Следовательно, если ошибки отсутствуют, Т(Х) делится на Р(Х) без остатка.

     Если один или более битов являются ошибочными, полученный блок Z(Х) будет иметь такой вид:

Z(X) = Т(Х) + Е(Х),

где Е(Х) — n-битовый полином ошибок, содержащий 1 в каждом двоичном раз­ряде, где в Z(Х) имеется ошибка. Если Z(X) передается через регистр LFSR, кото­рый показан на рис. 8.7, фактически производится деление Z(X)/P(X), что в результате дает синдром S(X) длиной (n-k) бит:

Скачать файл