Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов, страница 13

 При формировании каталогов из множества взаимосвязанных файлов, при организации программных комплексов или при проектировании вычислительных сетей часто возникает необходимость спроектировать граф виде дерева без циклов, петель и кратных ребер, но опирающийся на все множество исходных файлов, программных модулей или вычислительных станций. Такой граф называют покрывающим деревомили остовом. Построение остова графа G=<x, r> заключено в последовательном просмотре ребер графа в произвольном порядке и формировании фрагмента покрывающего дерева по алгоритму:

 шаг 1: выбрать любое ребро множества r, не являющееся петлей и сформировать фрагмент покрывающего дерева  G_i’=<X_i’,r_i’>,

а концевые вершины ребра включить в подмножество Х’;

шаг 2: выбрать любое ребро, не принадлежащее фрагменту и не являющееся петлей:

а) если одна концевая вершина выбранного ребра принадлежит фрагменту, то вторую концевую вершину включить в подмножество Х’, а ребро включить в фрагмент остова G_i’=<X_i’; r_i’^`>,

б) если ни одна концевая вершина ребра не принадлежит фрагменту остова, то сформировать фрагмент другого остова G_j’=<X_j’; r_j’^`>,

в) если концевые вершины принадлежат различным остовам, то объединить фрагменты, т. е.  G’=G_i’ÈG_j’, где X’=X_i’ÈX_j’, r’=r_i’Èr_j’,

г) если обе концевые вершины принадлежат фрагменту, то исключить это ребро;

шаг 3:  если все вершины графа вошли во фрагмент остова, т. е. X’=X то конец, иначе перейти у шагу 2.

Пример:  На рис. 28а) дан граф, а на рис. 28b) –его остов.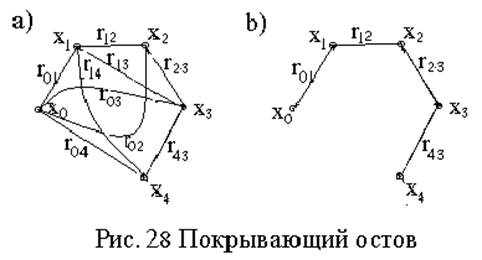

Процесс построения покрывающего дерева приведен в таблице.

Для пятивершинного графа потребовалось четыре шага итерации. При этом шесть ребер графа вообще не принимают участия в формировании остова. Иногда возникает задача не только найти покрывающий остов, но использовать определенный набор покрывающих ребер. Для этого  необходимо прежде всего определить цикломатическое число l(G), которое позволит знать число ребер, удаление которых ликвидирует циклы. Далее, используя элементы комбинаторики, найти число вариантов формирования остова. Для заданного графа l(G)=5, а число возможных пятивершинных четырехреберных графов, построенных на данном графе равно 126. Однако, среди них 10 графов сохраняют циклы. Следовательно, возможное число остовов данного графа равно 116, среди которых можно искать остовы удовлетворяющие особым требованиям.

3.4.2 Построение остова минимального веса

Решение этой задачи имеет большое значение в проектировании электрических, кабельных и трубопроводных сетей, в организации грузоперевозок по транспортной сети, в организации ремонтных работ на участках дорог и т. п..

Основная идея состоит в следующем: если есть некоторый фрагмент остова G’=<X’; r’^`> и ребро минимального веса l(х_i;х_j), одна из концевых вершин которого х_i принадлежит фрагменту G’, то включить в фрагмент вторую вершину ребра х_j и само ребро l(х_i;х_j). Процедуру продолжать до включения во фрагмент (n-1) ребра графа, где n-число его вершин. Такой граф будет обладать минимальным суммарным весом всех ребер остова. Эта идея реализуется двумя алгоритмами: Дейкстра и Краскала.

По алгоритму Дейкстра:

шаг 1: определить начальную вершину остова x₀;

шаг2: выбрать ребро минимального веса, смежное с начальной вершиной