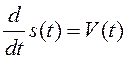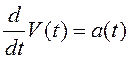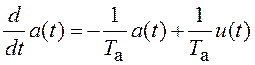Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики, страница 6

; ; .                       (3.38)

            Матрицы векторной формы формирующего фильтра равны

; .

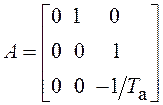Далее находим переходную матрицу с помощью выражения (1.37).

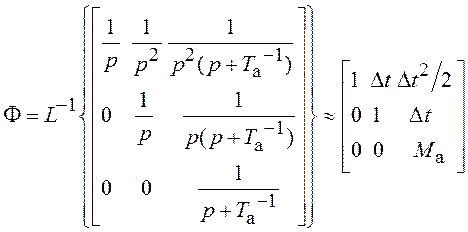            , где 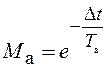.    (3.39)

При вычислении обратного преобразования Лапласа в выражении (3.39) было использовано разложение экспоненты в ряд при вычислении элементов третьего столбца  и .

 Выполняя расчет матрицы  с помощью выражения (3.20) получим результат, совпадающий с (3.30).                           

Используя выражения (3.19) и (3.39) получим систему разностных уравнений формирующего фильтра.

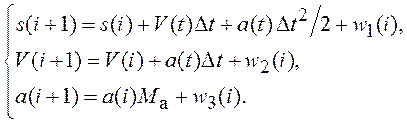                          (3.40)

            Полученные выше формирующие фильтры необходимы для исследования комплексных систем радиоавтоматики, построенных на совместном применении радиотехнических и автономных измерителей.

3.9. Анализ случайных ошибок систем РА во временной области

            Выполним анализ ошибок системы при действии случайного воздействия, формируемого из белого шума и наблюдаемого в смеси со случайной помехой (рис. 3.11).

            Формирование векторного воздействия описывается уравнением

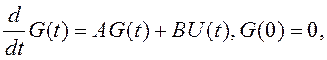                                             (3.41)                                       

где  – -мерный вектор;  – матрица размером ,  – матрица размером ,  –-мерный вектор белого гауссовского шума с нулевым средним и диагональной корреляционной матрицей .

            Наблюдаемый -мерный вектор  равен

,                                                             (3.42)

где  – матрица размером ;  –-мерный вектор белого гауссовского шума с нулевым средним и корреляционной матрицей .  

            Вектор  поступает на вход системы.

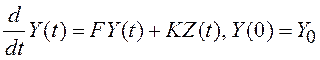,                                   (3.43)

где  – -мерный вектор;  – матрица размером ;  – матрица размером .

Произведем анализ ошибки системы .

            Затем, используя (3.41)–(3.43), составим дифференциальное уравнение для вектора ошибки.

.

            Из условия отсутствия смещения  следует

.                                                 (3.44)

            Такое же выражение было получено в задаче идеального наблюдателя. Используем это условие при составлении дифференциальных уравнений для вектора ошибки  и его  корреляционной матрицы .

.

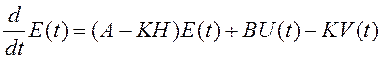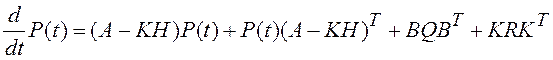, .      (3.45)      

Выполнив подстановку (3.44) в (3.43) получим уравнение системы, не имеющей смещения ошибки.

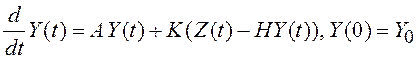.                                   (3.46)

Пример 3.4. Выполним расчет дисперсии ошибки системы с функцией передачи  при случайном воздействии в виде винеровского процесса, наблюдаемого при действии помехи.

 Уравнение (3.41) в данном случае принимает вид

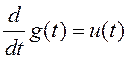, где  – белый шум с корреляционной функцией .

Уравнение наблюдения (3.42) имеет вид , где  – белый шум с корреляционной функцией .

Используя (3.31) при условии  составим уравнение системы

  .

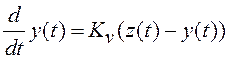В примере , , , , . Тогда  и .

Используя дисперсионное уравнение (3.45) получим

.

Решение этого уравнения равно

.

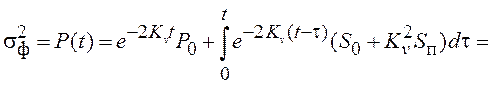
При  получим 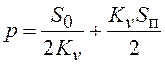. Первое слагаемое этого выражения повторяет результат, полученный в примере 3.3 частотным методом (без действия помехи), но решение во временной области позволяет исследовать переходный процесс.

3.10. Анализ случайных ошибок дискретных систем РА во временной области

Произведем анализ ошибок системы в дискретном времени при действии случайного воздействия , формируемого из случайного процесса  и случайной помехи  (рис. 3.12).

            Разностные уравнения процесса  и наблюдения  описывают дискретный эквивалент формирующего фильтра (3.41) и наблюдения (3.42).

,                               (3.47)

,                                                     (3.48)

где –-мерный вектор;  – матрица размером ;  – случайный -мерный вектор дискретного белого гауссовского шума с нулевым средним и корреляционной матрицей ;  – -мерный вектор;  – матрица наблюдения  размером ;  – случайный -мерный вектор дискретного белого гауссовского шума с нулевым средним и корреляционной матрицей .

            Разностные уравнения вектора состояния системы  имеют вид