Сходимость по метрике. Полнота метрических пространств. Принцип сжимающих отображений и его применение. Нормированные пространства, страница 6

На множестве B_F функций, имеющих конечное (финитное) преобразование Фурье (для любой функции, принадлежащей B_F,
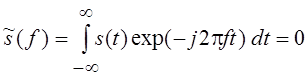 при | f| > F), базисную систему образует совокупность функций 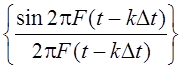, называемая базисом Котельникова. Номера функций k = 0, ± 1, ± 2, … , а 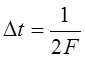. Данное утверждение означает, что " s(t) ÎB_F  можно записать

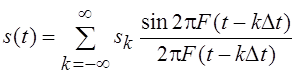.                                  (3.1)

Далее будет показано, что координаты , т. е. являются значениями функции s(t), взятыми в моменты времени  и называются отсчетами функции s(t).

Для бесконечномерных ЛП выбор базисной системы зависит от используемой метрики. Так, при использовании в L метрики  линейно независимая система функций , k = 0, 1, 2, … является базисом, если для " s(t) Î L справедливо представление

.                                             (3.2)

Если используется евклидова метрика  и в качестве ЛП выбирается , то для того, чтобы совокупность линейно независимых функций , k = 0, 1, 2, … была бы базисом, необходимо выполнение следующего условия:

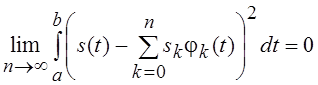" s(t) Π.                  (3.3)

Стремление 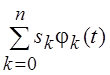 к s(t) при п ®¥ в смысле (3.3) называют сходимостью в среднем. Заметим, что выполнение (3.3) не гарантирует справедливость (3.2). Для этого на функции, принадлежащие , должны быть наложены дополнительные ограничения, о которых речь пойдет ниже.

В  базисную систему образует совокупность функций 1, cos t, sin t, cos 2t, sin 2t, …, называемая тригонометрической системой функций.

При этом для  " s(t) Πможно записать тригонометрический ряд вида 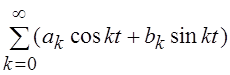, который при соответствующем выборе коэффициентов a_k и b_k сходится к s(t) в смысле метрики , т. е. в среднем.

Из приведенных примеров видно, что использование базиса в функциональных пространствах позволяет заменить функцию (аналоговый
сигнал) совокупностью чисел, что является основой цифровой обработки сигналов.

Отметим, что базисная система в ЛП не является единственной. Одним из способов получения новых базисных систем на основе имеющейся является линейное комбинирование векторов исходной системы. Две системы, каждый вектор которых есть линейная комбинация векторов другой системы, называются эквивалентными. Позже мы познакомимся с одной из таких процедур, называемой процедурой Грама–Шмидта.

Контрольные вопросы

1.  Дайте определение линейного пространства.

2.  Приведите примеры линейных пространств.

3.  Дайте определение линейной комбинации векторов из L.

4.  Дайте определение линейной независимости системы векторов , i = 1, 2, …, n; .

5.  Как определяется размерность линейного пространства?

6.  Дайте определение базиса конечномерного ЛП.

7.  Как определяется базис для бесконечномерных метрических ЛП?

8.  Приведите примеры базисных систем для различных линейных пространств.

9.  Дайте определение линейного подпространства.

10.   Что называется линейной оболочкой системы векторов , i = 1, 2, …, n?

11.   Что является линейной оболочкой системы базисных векторов?

12.   Образует ли линейное подпространство совокупность векторов на плоскости, начало которых лежит в точке (1, 1), а концы не выходят за пределы квадрата с вершинами в точках (1, 1), (1, 2), (2, 2) и (2, 1)?

ГЛАВА 4. ЕВКЛИДОВЫ ПРОСТРАНСТВА

Евклидово пространство связано с введением понятия скалярного произведения, обобщающего для произвольных пространств процедуру измерения угла между двумя векторами. В самом деле, из аналитической геометрии хорошо известно, что скалярным произведением двух векторов  и  является произведение их длин (модулей) || и || на косинус угла между ними, т. е.

; .

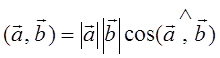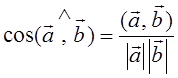Обобщением понятия модуля вектора является введенная выше норма вектора ||||. Таким образом, учитывая, что 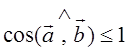, получим

,                                               (4.1)

что представляет собой неравенство Коши–Буняковского.

Неравенство (4.1) обращается в равенство, если , т. е., если вектора являются коллинеарными (параллельными). Аналитически условие коллинеарности векторов  и записывается как

 = a, a Î R.                                              (4.2)

Ниже неравенство (4.1) и условие (4.2) будут получены для произвольных ЛП.