Сходимость по метрике. Полнота метрических пространств. Принцип сжимающих отображений и его применение. Нормированные пространства, страница 2

2.2. Сходимость по метрике. Полнота метрических пространств

Говорят, что последовательность элементов  метрического пространства (Х, r) сходится к элементу хÎХ, если .

Последовательность  элементов  метрического пространства (x, r) называется фундаментальной или последовательностью Коши, если  такое, что из условия n,m > N следует, что .

Из аксиомы 3 следует, что любая сходящаяся последовательность является последовательностью Коши. Обратное утверждение в общем случае неверно, так как для последовательности Коши предельный элемент может не принадлежать метрическому пространству Х.

Рассмотрим пример, иллюстрирующий приведенное утверждение. Пусть на множестве С непрерывных на промежутке [0, 1] функций рассматривается последовательность функций вида

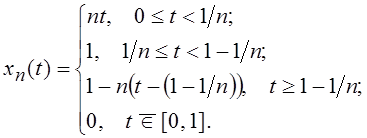
Если на данном множестве задать евклидову метрику , то данная последовательность будет фундаментальной, так как  такое, что при n,m > N выполняется неравенство 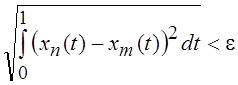. Но последовательность x_n(t) не является сходящейся, так как предельный элемент, прямоугольная функция, не принадлежит С, поскольку в точках 0 и 1 нарушаются условия непрерывности.

Метрическое пространство, в котором каждая последовательность Коши сходится, называется полным метрическим пространством.

Рассмотренный выше пример позволяет утверждать, что множество функций, непрерывных на сегменте [0, 1], с евклидовой метрикой не является полным метрическим пространством. С другой стороны можно показать, что это же множество при задании метрики равномерного приближения 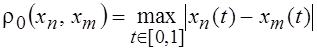 является полным метрическим пространством.

Метрические пространства, рассмотренные в примерах 1 – 7 предыдущего раздела, за исключением примера 6, о котором только что шла речь, являются полными.

Важным понятием, связанным с метрическим пространством, является понятие множества, плотного в рассматриваемом метрическом пространстве. Пусть Х – метрическое пространство. Множество Х₀ Ì Х  является плотным в Х, если  такой, что . Это эквивалентно утверждению, что для любого х Î Х существует последовательность Ì Х₀  такая, что .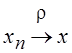

Если множество Х₀, плотное в Х, является счетным, то метрическое пространство Х  называется сепарабельным.

Примерами сепарабельных пространств могут служить R_n, C[a, b]. Для R_n плотным множеством является совокупность п-мерных векторов с рациональными элементами, а  для C[a, b] это множество алгебраических многочленов с рациональными коэффициентами, которыми в соответствии
с теоремой Вейерштрасса можно равномерно, т. е. по метрике 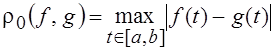, аппроксимировать любую непрерывную на [a, b] функцию.

2.3. Принцип сжимающих отображений и его применение

Многие задачи, в том числе и связанные с радиотехникой, решаются с помощью итерационной процедуры, в основе которой лежит принцип сжимающих отображений.

Отображением называют правило А, по которому каждому элементу х одного непустого множества Х ставят в соответствие некоторый элемент у непустого множества Y. Это сопоставление записывается как А: Х® Y для множеств или как у = А(х) (иначе, у = Ах) для элементов.

Часто отображение действует в одном и том же множестве, т. е. исходные элементы (прообразы) и получаемые при отображении (образы) принадлежат одному и тому же множеству Х. Такое отображение можно записать как x’ = Ax’’, где x’, x’’ÎХ.

Сформулируем теперь  принцип сжимающих отображений. Пусть Х – метрическое пространство с метрикой r. Отображение А пространства Х в себя называется сжимающим отображением, если $ (a <1) такое, что для
"( x’, x’’ÎХ) выполняется неравенство

r(А x’, Аx’’)£ar(x’, x’’)                                       (2.1)

Из определения (2.1) видно, что всякое сжимающее отображение непрерывно, так как из 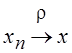 следует .

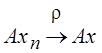Точка х называется неподвижной точкой отображения А, если Ах = х,
т. е. неподвижная точка – это решение уравнения

Ах = х.                                                     (2.2)

Справедлива теорема: всякое сжимающее отображение, определенное в полном метрическом пространстве Х, имеет одну и только одну неподвижную точку. Иными словами, существует единственное решение х^* уравнения (2.2), которое может быть получено как предел последовательности , где

х_п = Ах_п–1, п = 0, 1, … ,                                       (2.3)

а х₀ – произвольный элемент из области определения оператора А. При этом скорость сходимости итерационной процедуры (2.3) определяется неравенством