2.
В Rn в соответствии с
введенными выше метриками можно определить ||![]() ||0 =
||0 =![]() , ||
, ||![]() ||1 =
||1 =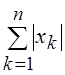 , ||
, ||![]() ||2 =
||2 =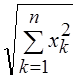 .
.
3.
Для пространства C[a,
b] обычно используется || f ||0
=![]() , а для L2[a, b] применяется || f ||2 =
, а для L2[a, b] применяется || f ||2 =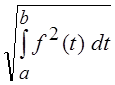 .
.
Для
комплекснозначных пространств в соответствии с аксиомами нормы и метрики
используются соотношения ||![]() ||2 =
||2 =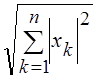 и || f ||2
=
и || f ||2
=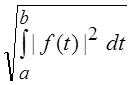 .
.
Заканчивая разговор о метрике и норме, отметим, что в геометрии способ задания метрики определяет геометрическую систему. Так, на искривленной поверхности расстояние между двумя точками с декартовыми координатами xi, yi и xj, yj в общем случае определяется как
![]() ,
,
где Dх = xi – хj, Dy = yi – yj, а система чисел gxx, gxy, gyx, gyy образует фундаментальный метрический
тензор, полностью определяющий геометрическую систему. Так, при gxx, = gyy = 1 и gxy = gyx выполняется соотношение ![]() ,
характеризующее систему (геометрию) Евклида. Планиметрии Лобачевского,
построенной на поверхности, напоминающей грамофонную трубу, и планиметрии
Римана, построенной на сфере, соответствуют другие значения чисел, определяющих
фундаментальный метрический тензор.
,
характеризующее систему (геометрию) Евклида. Планиметрии Лобачевского,
построенной на поверхности, напоминающей грамофонную трубу, и планиметрии
Римана, построенной на сфере, соответствуют другие значения чисел, определяющих
фундаментальный метрический тензор.
2.5. Пространства с мерой
Пусть S – рассмотренная в 1.4 s-алгебра, и каждому множеству, входящему в S, ставится в соответствие вещественное число j(Ai), где Ai Î S, т. е. задано отображение S®R, причем для любой счетной совокупности попарно непересекающихся множеств Ai Î S выполняется равенство
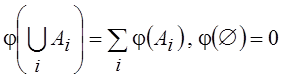 .
.
Определенная таким образом функция j называется счетно-аддитивной функцией множества. Если выполняется условие j(Ai) ³ 0 для любого Ai Î S, то j неотрицательна.
Рассмотренные понятия являются ключевыми при аксиоматическом построении теории вероятностей [6]. Центральным понятием в теории вероятностей является вероятностное пространство {W, S, Р}, т. е. совокупность трех объектов – пространства элементарных событий W, которому в наших предыдущих рассуждениях соответствует единица, s-алгебры S подмножеств пространства W, называемых случайными событиями А, а также вероятностной меры Р(А), определенной для всех А Î S, называемой вероятностью случайного события А, причем Р(W) = 1.
Из свойств меры следует, что вероятность объединения несовместных событий Ai Î S равна сумме вероятностей объединяемых случайных событий:
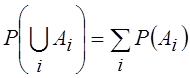 .
.
Контрольные вопросы
1. Дайте определение метрического пространства.
2. Сформулируйте аксиомы метрики.
3. Приведите примеры метрических пространств.
4. Проверьте аксиому треугольника для пространства изолированных точек.
5. Приведите примеры метрик, задаваемых на множестве непрерывных на [a, b] функций.
6. Как определяется евклидово расстояние в Rn, l2, L2?
7. Что такое евклидово расстояние с весом?
8. Дайте определение полноты метрического пространства.
9. Что такое сепарабельное метрическое пространство? Приведите примеры.
10. Сформулируйте принцип сжимающих отображений.
11. Что называется неподвижной точкой отображения А метрического пространства Х в себя?
12. Как записывается итерационная процедура отыскания неподвижной точки и чем определяется скорость ее сходимости?
13. Дайте определение нормированного пространства.
14. Как задается метрика в нормированных пространствах?
15. Как определяется норма в l2?
ГЛАВА 3. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
Линейные пространства, называемые также иногда векторными, относятся к числу важнейших математических структур, широко используемых в самых различных приложениях. Их элементы называют векторами или точками.
Линейные пространства (ЛП) строятся над произвольными полями F, элементы которых, называемые скалярами, используются для построения векторов (элементов ЛП). Наиболее часто используются поля вещественных или комплексных чисел. В соответствии с этим говорят о действительных или комплексных ЛП.
Определение. Непустое множество L элементов ![]() ,
,
![]() ,
, ![]() , … (L может быть конечным, счетным или
несчетным, его элементы могут быть векторами в обычном понимании этого слова,
матрицами или функциями) называется линейным или векторным пространством, если
выполняются следующие условия, называемые аксиомами ЛП:
, … (L может быть конечным, счетным или
несчетным, его элементы могут быть векторами в обычном понимании этого слова,
матрицами или функциями) называется линейным или векторным пространством, если
выполняются следующие условия, называемые аксиомами ЛП:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.