Конспект лекций по дисциплине "Высшая математика", страница 37

таким образом внешняя форма дифференциала  не изменяется, если переменная и функции у есть, в свою очередь, функция аргумента х. Такое свойство дифференциала  называется инвариантностью.

Производные  высших порядков

Определение  Производной высшего порядка от функции  называется производная порядка выше первого, т.е. , при этом

Примеры  1) Найти , если 

;   ;  ;   .

2) Найти , если 

;  ;  ;  ;  .

Правило Лопиталя

Рассмотрим отношение  , где функции  и определены и дифференцируемы в некоторой окрестности точки , исключая, быть может саму точку .

Пусть эти функции одновременно являются бесконечно малыми или бесконечно большими при .

Теорема  Предел отношения двух бесконечно малых или бесконечно больших функций при  равен пределу отношения их производных, если последний существует, т.е.

.

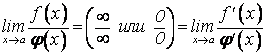Правило Лопиталя применяется любое конечное число раз, пока существует неопределенность  или .

Примеры  1.

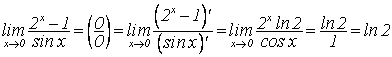
2.

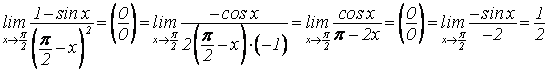
3. .

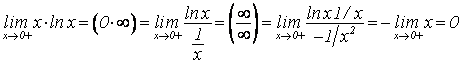Общая схема исследования функции

1. Область определения функции  - совокупность тех значенийх, при которых  вычисляется действительным конечным числом (или определена, или существует).

Если существует точка , в которой  не определена, то необходимо вычислить односторонние пределы функции , . Если хотя бы один из них бесконечный, то в точке   имеет разрыв II рода.

Определение  Асимптотой кривой  называется прямая линия (вертикальная , наклонная , горизонтальная ), к которой неограниченно приближается точка кривой, удаляясь по кривой от начала координат в бесконечность.