Линейные операторы и функционалы. Часть 1, страница 6

Важным типом линейных операторов являются нормальные операторы. Оператор А называется нормальным, если он коммутирует со своим сопряженным, т. е. АА^* = А^*А. Частным случаем нормальных операторов являются рассмотренные выше самосопряженные операторы, для которых А^* = А. Другим частным случаем нормальных операторов являются унитарные операторы.

Унитарным оператором U называется линейный оператор, преобразующий Н на все Н и не меняющий нормы преобразуемых векторов, то есть . Унитарный оператор имеет обратный U ^–1 и U ^–1= U^*. Таким образом, U U^* = U U ^–1 = U^*U = U ^–1U = Е. Унитарный оператор не меняет скалярного произведения так как .

Легко доказать, что произведение унитарных операторов есть также унитарный оператор, а оператор, обратный унитарному оператору также унитарен. Таким образом, унитарные операторы образуют группу. Сформулируем следующее важное свойство унитарных операторов. Собственные значения унитарного оператора по модулю равны единице, а собственные вектора соответствующие различным собственным значениям ортогональны.

Для дальнейшего изложения нам понадобится понятие дельта-функции, которое мы введем, пользуясь терминологией теории вероятности. Пусть W_x(x) плотность вероятности (ПВ) случайной величины (СВ) x, имеющая производные любого порядка. Например, 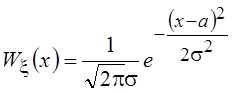, где а – математическое ожидание (среднее значение) СВ x, а s² – ее дисперсия.

Будем считать, что а = 0 и определим обобщенную функцию d(х), называемую дельта-функцией Дирака или просто дельта-функцией как . Так как по условию нормировки 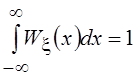, это свойство сохраняется и для дельта-функции, т. е. .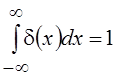

Интеграл от дельта-функции с переменным верхним пределом 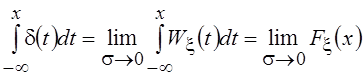, где F_x(x) – функция распределения (ФР) СВ x. Функция  определяет функцию единичного скачка Хевисайда .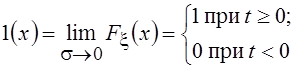

Таким образом, с точки зрения теории вероятности дельта-функция и функция Хевисайда определяют ПВ и ФР детерминированной случайной величины Х принимающей единственное значение х = 0.

Запишем основное интегральное соотношение для дельта-функции, определяющее ее "фильтрующее" свойство.

Для любой непрерывной функции f(t) интеграл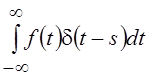 с учетом того, что дельта-функция отлична от нуля лишь в точке s = t, можно записать как 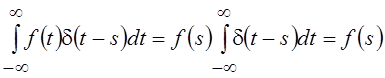 так как 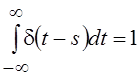. Считая правомерным дифференцирование интеграла 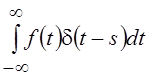 по параметру s, получим 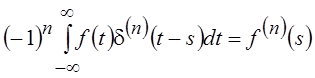 или, окончательно,

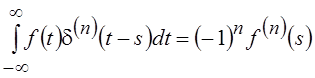, n = 0, 1, ….

Тем самым определено понятие производной дельта-функции. Более глубоко с теорией обобщенных функций можно ознакомиться с помощью [8].

Выясним условия, при которых оператор Фредгольма
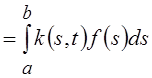 будет унитарным оператором. Запишем скалярное произведение преобразованных функций, имея в виду общий случай комплексного Н-пространства со скалярным произведением 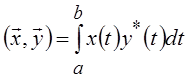. Тогда

.

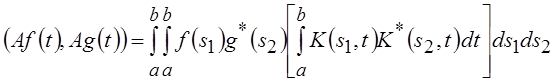Если потребовать, чтобы

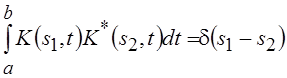,                                  (5.4)

где  – дельта-функция, то учитывая "фильтрующее" или интегральное свойство дельта-функции, получим 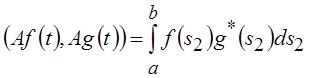. Таким образом, условие (5.4) обеспечивает унитарность оператора А. 

Заканчивая обзор линейных операторов, остановимся на одном линейном операторе, который часто встречается в задачах радиотехники. Это оператор проектирования.

Оператором проектирования в Н на пространство М ÌН называется отображение  на вектор , такое, что , где . Запись  означает, что  ортогонален любому вектору из М.

Оператор проектирования обычно обозначают как Р, указывая иногда с помощью индекса подпространства, на которое осуществляется проектирование, т. е. пишут Р_М. Очевидно, что норма || P || = 1 (доказать самостоятельно).

Ключевым свойством оператора проектирования является справедливость утверждения Рⁿ = Р, т. е. многократное применение оператора проектирования совпадает с однократным. Оператор проектирования является самосопряженным. Для того, чтобы линейный оператор Р в Н был проектором,