Линейные операторы и функционалы. Часть 1, страница 2

Сумма и произведение линейных операторов.

Суммой линейных операторов А и В называют линейный оператор С, для которого . Область определения оператора С является пересечением областей определения операторов А и В.

Если операторы А и В ограничены, то .

Произведением операторов А и В называют результат их последовательного действия, т. е. . Область определения С состоит из тех , для которых , где D_B и D_A – области определения операторов В и А соответственно. На основании введенных определений ясно, как определять степень оператора A^k и функцию от оператора 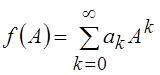, представленную с помощью степенного ряда. По определению полагают .

Спектр оператора.

Мы уже отмечали, что наличие у оператора А обратного А^–1 позволяет утверждать, что уравнение  разрешимо относительно  при любом . Часто вместо этого уравнения рассматривают уравнение  , где l – числовой параметр. Это уравнение можно переписать в форме

,                                             (5.1)

где Е – тождественный (единичный) оператор. Одновременно с уравнением (5.1) рассматривают уравнение

,                                             (5.2)

которое называют однородным уравнением для уравнения (5.1). Если для данного значения l оператор А – lЕ имеет обратный (А – lЕ)^–1 = R_l, называемый разрешающим оператором или резольвентой, то уравнение (5.1) имеет при любом  решение и при том только одно. Тогда однородное уравнение (5.2) при данном l имеет лишь нулевое решение. Такие значения l называются регулярными значениями оператора А. Все значения параметра l, не являющиеся регулярными, образуют спектр оператора А.

Среди значений параметра l, образующих спектр, могут быть такие значения l₀, l₁, …, l_n, …, при которых однородное уравнение (5.2) имеет ненулевые решения . Такие значения параметра называются собственными значениями или характеристическими числами, а соответствующие им вектора  –  собственными векторами оператора А. Совокупность собственных значений называется дискретным (точечным) спектром оператора А.

Пример 1. Мы уже отмечали, что в конечномерных пространствах действие любого линейного оператора сводится к умножению вектора  на матрицу оператора А = {a_ij}. Уравнение (5.1) в этом случае превратится в систему линейных уравнений вида

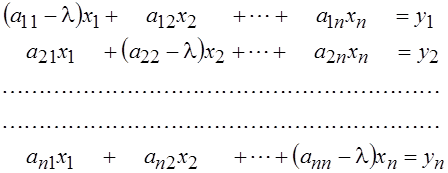.                   (5.3)

Мы считаем в данном случае, что Х = Х ' = Y = Y ', т. е. оператор А действует из Х в Х и матрица оператора квадратная. Если определитель этой системы 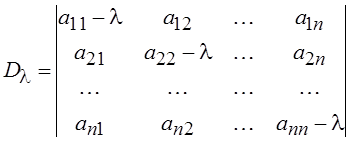 отличен от нуля, то есть l не является корнем уравнения D(l) = 0, называемого характеристическим, то записанная система уравнений имеет единственное решение при любых  (правых частях) и все такие значения параметра l регулярны. Корни уравнения D(l) (их не более n) образуют спектр. Так как при этих значениях l однородная система,  соответствующая (5.3), имеет нетривиальное решение (отличное от нуля), то любая точка спектра является собственным значением. 

Таким образом, характеристические числа, или собственные значения линейного оператора в конечномерном пространстве являются корнями характеристического уравнения  D(l) = 0, а решения однородной системы для каждого собственного значения дают собственные вектора оператора.

Пример 2. Для дифференциального оператора D₂ y(t) = y''(t)+ ly(t), описывающего колебательный контур без потерь, собственные значения равны  а соответствующие им собственные вектора (в данном случае функции) равны exp (jlt) и exp (–jlt) соответственно.

Линейные функционалы и операторы в Гильбертовом пространстве.

Определим  на ЛП L числовую функцию , отображающую вектора из L в скаляры из поля F, над которым задано L. Выражение  называется линейным функционалом, если справедлив принцип суперпозиции, состоящий в том, что для любых , Î L  и

,

включающий в себя аддитивность  и однородность .

Приведем примеры линейных функционалов.